[科普中国]-自适应选择

自适应选择

首先根据终端设备获取所有可适应的网络；然后判定该网络是否可以启动自适应，从而将可启动自适应的网络按照所设置的自适应网络方式的优先顺序进行记录；接着启动自适应，则终端设备将通过所记录的优先顺序，将选择的最优先无线网络同当前使用的网络类型进行比较，如果相同，则不进行切换，否则切换到最优先的无线网络；重复上述步骤直至找到最佳或需要的网络环境。

自适应就是在处理和分析过程中，根据处理数据的数据特征自动调整处理方法、处理顺序、处理参数、边界条件或约束条件，使其与所处理数据的统计分布特征、结构特征相适应，以取得最佳的处理效果的过程。

自适应过程是一个不断逼近目标的过程，它所遵循的途径以数学模型表示，称为自适应算法。通常采用基于梯度的算法，其中最小均方误差算法(即LMS算法)尤为常用。1

自适应算法可以用硬件(处理电路)或软件(程序控制)两种办法实现。前者依据算法的数学模型设计电路，后者则将算法的数学模型编制成程序并用计算机实现。算法有很多种，它的选择很重要，它决定处理系统的性能质量和可行性。常用的自适应算法有迫零算法，最陡下降算法，LMS算法，RLS算法以及各种盲均衡算法等。

例如，自适应均衡器就是按照某种准则和算法对其系数进行调整最终使自适应均衡器的代价(目标)函数最小化，达到最佳均衡的目的，而各种调整系数的算法就称为自适应算法。

自适应算法是根据某个最优准则来设计的。自适应算法所采用的最优准则有最小均方误差(LMS)准则，最小二乘(LS)准则、最大信噪比准则和统计检测准则等。LMS算法和RLS算法由于采用的最优准则不同，因此这两种算法在性能，复杂度等方面均有许多差别。

预测模型的自适应选择模型函数，有很多简单模型，实际上，有些也更加复杂的多。这些模型的判别、识别、参数估计和选择工作十分繁重，也十分复杂。有时能够用于某种经济预测对象的模型方法有很多中，例如以上的模型例子都可以用于经济序列的预测分析。这种情况下，如何选择；如何比较；以什么为参考标准；到底哪一种方法可行；哪一种最好等都是令工程技术人员头痛的事情。因此，我们有必要设计一种自适应的模型比较和选择的方法过程，建立一套智能化的预测分析软件，为工程和经济预测分析的良好应用提供方法及工具。

我们知道，对信息数据或样本进行背景分析，根据数据信息所反应出的结构和趋势特点，选择相应的预测模型组是进行智能预测分析的第一步。经济数据背景分析的方法很多，例如可以将数据进行差分分析，增量分析，迭加分析等，通过这些计算分析可以判断出信息数据是否具有线性特征，指数特征，生长曲线特征，周期特征以及多种组合特征等。在加上数据的背景分析，可以容易地对其作出一定的解释。

特性通过对经济数据的详细计算分析，可以发现数据序列的以下特性：

(1)数据序列的递增或递减性，即数据的趋势特征；

(2)数据的某种周期性变化特征；

(3)经济数据的变化强度和相关性；

(4)数据的随机变化特征；

(5)多种趋势曲线成份特征；

(6)数据序列发展变化的局部极值点和极限；

(7)数据的一致性特征，即数据的稳健性；

(8)数据的相关背景特征等。但这还远远不够，有的预测方法，由于其数学结构的复杂性，从简单的背景分析中是计算不出来的。所以，我们应该罗列所有可用的预测模型方法，在经济预测中，建立一个尽可能丰富的模型库，这是智能化预测软件的基础。对于同一个经济预测对象，可以有许多不同的预测模型可用，那么用那一种好呢?这就是我们要在智能化预测中试图解决的问题。

模型自适应选择方法背景分析对数据进行背景分析、必要的稳健性处理。通过背景分析把握两个问题：

一是背景情况、数据的可靠性和可用性；

二是确定预测分析所用的预测方法的大类，如回归模型、时间序列模型还是计量模型，以及投入产出模型等。当发现有异常值，而且需要进行处理后，才能用时，就需要对数据进行稳健预处理。

模型方法库建立丰富的模型方法库，并将这些模型方法分类，例如时间序列模型，内容包括各种各样的趋势模型、周期模型，以及混合模型等。

根据数据构成的特点，选择相应的建模方法，进行预测分析。但有的预测可以直观地根据预测目标确定预测方法，例如，设备状态的预测，简单的天气预测，就可以直接用MARKOV(马尔可夫)预测方法进行。许多像这样的预测，带有明显的范围特点，此时可以直接选用适用此类预测目标的固定预测方法。

回归预测方法也带有明显的结构特征。此时，历史数据通常表现为有一个数据(一元回归)或几个数据(多元回归)决定一项预测目标，历史数据同时有好几个序列组成。在这种情况下，主要是判别是线性回归还是非线性回归。线性回归的分析方法采用LS估计，比较简单，方法也比较成熟。

而非线性回归，我们可以通过神经网络预测法来分析，采用BP三层网络算法进行逼近，然后，将各种方法预测结果的方差进行比较分析，根据各方面综合分析之结果确定采用回归预测的类型。

在许多连续预测中，我们还应研究一种自适应预测方法，这种方法能够适时地根据预测误差及时调整预测方法。这样能保证预测的最适性。

如果数据背景分析的结果表明，历史数据的变化呈现某种曲线的趋势，我们可以选用近似而光滑的连续函数来分析。这些函数应尽可能的简单，即要求函数项少，幂次低，极值及拐点少。

趋势外推函数

根据具体背景分析情况，常用的趋势外推函数有以下几种：

(1)线性型；

(2)二次型；

(3)指数型；

(4)双曲线型；

(5)生长曲线型；

(6)周期曲线型等：

这些模型当具体的预测对象明确之后，也就是说知道了预测方法的大类后，尽可能多的寻找可用的方法模型．建立一个可选的模型组。

建立判别理论基础为了比较选择一种相对最合适的模型，必须建立判别、比较的标准。通常情况下人们选择拟合的方差(最小二乘估计、统计检验等方法都是建立在最小方差的基础上)作为一种判断的标准。在选择预测方法时，因为预测是对未来经济事物的推测，不可避免地要产生误差，误差大小说明预测的精度，是评价预测好坏的重要标准，因此在选择预测方法时，应使误差尽可能的小。方差越小，预测精度也越高。这是常规性原则。

除了我们用均方差来衡量预测效果的好坏之外；在实用中，我们还应结合其他的判别方法，例如，随机误差的信息熵H(r)和其它的经验公式等。利用这些理论方法来判别预测方法的可用性。

我们可将均方差MSE(f)分解为三个部分，这可以进一步说明系统误差的来源，而且还可以帮助预测工程技术人员得到更详细的依据，以及认清系统误差的不同来源。

均方差可分为三项：

第一项是偏差平方，它反应了由于真正偏差引起的预测误差；

第二项是以斜率余数平方和做权数引起的预测误差，它反应了斜率的误差；

第三项是以实际值与预测判别系数的余数为权数的实际方差，它反应了误差中有残差部分。

了解误差的构成，有助于分析经济预测分析过程中的误差源，并设法减小。有的情况下，我们不但要用均方差来判别，而且还要衡量误差序列的离散程度。我们将误差序列看作随机变量

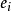设为其概率分布密度，则正的熵为，的各项积分和，计为。由信息论知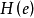，反应了随机变量E的不确定程度。因此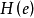，也说明了预测的不确定程度或者预测的准确程度。预测熵对于所选择的预测方法从另外一个角度说明了其实用性，这一点在人工神经网络应用于经济预测分析时非常有用。

我们还可考虑引入其他的标准，来反应不同的方法对一个经济数据的可预测度，这也是一个值得研究的技术问题。因为，预测技术人员可能面对来自各行各业的经济数据列，这些数据既有线性也有非线性，甚至有混沌现象。所以，可预测度问题也必须予以考虑。对于一个可预测性较差的信息数据列，即使人们临时找到的预测方法很好，预测精度一时很高，其长期的适用性也可能有问题。

我们可考虑定义一个可预测度参数，设为P0，一个方法的P越大，表示它的可预测度越高，因此，我们可以用户来反应预测模型可测性的好坏或强弱；同时也反应预测模型对所研究的经济预测系统的控制能力及经济系统发展的不确定性。

简单的判别不太全面，也不科学，在对具体经济问题预测分析时，需要建立全面科学的判别根据，这就是我们所说的统一判别理论，也是智能预测判别分析的理论标准，当然也是智能预测研究的关键问题。

关于统一的判断理论标准是一个需要进一步研究的课题。当然，目前在我们的方法中．用的还是最小方差的判别方法，即在一群模型组中，比较拟合的方差，选择其中拟合方法最小的模型。