[科普中国]-泰勒假设

简介

泰勒(Taylor)提出在满足某些条件的情况下，当湍流流经传感器时，可以认为湍流是被冻结的.其含义是在空间上一固定点对湍流的观测结果统计上等同于同时段沿平均风方向空间各点的观测，也称为定型湍流假设，当然湍流并不是真的被冻结，只是假设湍涡发展的时间尺度大于它被平流携带经过探头所需的时间，泰勒假设才适用。1

原理我们常常需要边界层湍涡大小和运动尺度方面的信息，遗憾的是，要得到一张边界层快照是很难的。我们发现，对空间某一点进行长期测量比较容易，而要进行瞬时的大范围观测却很难。例如安装在观测塔上的气象仪器，当湍流通过传感器时，便能为我们提供一张边界层随时间变化的记录。

1938年G.I.泰勒假设，在某些特定情况下，当湍流平移过传感器时，可以把它看成是凝固的。这样，风速就可以用来把本来作为时间函数对湍流的测量变为相应的空同上的测量。我们应当考虑湍流并不是真正凝固的，因此，泰勒的简化假说只能用于湍涡发展的时间尺度大于其平移过传感器的时间。2

公式利用风速ū与时间t的乘积等于该空气团运行距离x=ūt的关系，可将时间序列的湍流资料转化为相应的空间测量资料，其中ū为平均风速，选择x沿主导风速方向。

对于任意变量ω，泰勒假设可表述为：当dω/dt=0时，湍流是冻结的、因此泰勒假设的一般形式为：

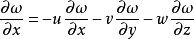
其中u，v和w分别为x，y和z方向的风速分量。1

适用条件泰勒假设虽然一直没有得到严格的证明，而且此假设中实际还隐含着平稳气流和均匀湍流的条件，风速也不宜过小，但根据实际观测资料的验证，泰勒假设在边界层中是适用的。1