[科普中国]-多指标非线性控制

背景

电力系统非线性控制在80年代末、90年代初被提出。由于该方法可对受控系统进行非线性变换，实现系统的大范围精确线性化，解决了以往采用局部线性化带来的控制器性能受运行条件变化影响的问题。因此，这种控制方式一经提出就受到了广大科技工作者的极大关注。

发电机是电力系统中的一个最主要的设备，因此非线性控制设计在电力系统中的应用首先是从发电机的非线性控制设计开始的。经典的发电机控制模型具有两个控制量，分别是励磁控制和原动机(汽门或水门)控制，早期的电力系统非线性控制运用研究主要是针对单输入单输出控制系统进行的，发电机的非线性励磁控制问题最先被提出来，并且在进行励磁控制设计时，假设在励磁调节过程中，发电机的原动机控制不发生变化。由于最初普遍认为，非线性控制设计的优点在于该方法能将受控系统在平衡点进行大范围线性化，因此设计工作的重点是寻找能将发电机励磁系统的数学模型完全精确线性化的变换。按照严格的数学理论，人们终于找到了能将发电机励磁控制系统完全精确线性化的输出函数是

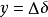
发电机励磁控制完全精确线性化设计的成功，是非线性控制设计方法在电力系统应用中的一个有代表性的研究成果，它推动了非线性控制在电力系统中的应用。

但是在随后的研究中，人们就发现按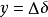为输出函数设计的非线性励磁控制律，无法精确地将发电机的端电压控制在给定值上运行。当发电机的有功输出发生变化时，发电机的端电压将发生偏移，并且无法由该非线性控制律将发电机的端电压调节回原给定值运行。这意味着发电机端电压在该非线性控制律的作用下会产生静态偏移。而对于发电机来说，工业运行中主要关心的有三个量，即端电压Uf，转速ω和输出有功Pe。其中对端电压只能通过调整励磁控制来保证，因此，如果该非线性励磁控制律无法保证发电机在运行过程中的控制精度，也就没有其它办法可用来解决发电机的机端电压静态偏移问题。

非线性系统非线性系统：一个系统,如果其输出不与其输入成正比，则它是非线性的。从数学上看，非线性系统的特征是叠加原理不再成立。叠加原理是指描述系统的方程的两个解之和仍为其解。叠加原理可以通过两种方式失效。其一，方程本身是非线性的。其二,方程本身虽然是线性的,但边界是未知的或运动的。

意义“线性”与“非线性”是两个数学名词。所谓“线性”是指两个量之间所存在的正比关系。若在直角坐标系上画出来，则是一条直线。由线性函数关系描述的系统叫线性系统。在线性系统中，部分之和等于整体。描述线性系统的方程遵从叠加原理，即方程的不同解加起来仍然是原方程的解。这是线性系统最本质的特征之一。“非线性”是指两个量之间的关系不是“直线”关系，在直角坐标系中呈一条曲线。最简单的非线性函数是一元二次方程即抛物线方程。简单地说，一切不是一次的函数关系，如一切高于一次方的多项式函数关系，都是非线性的。由非线性函数关系描述的系统称为非线性系统。

区别定性地说，线性关系只有一种，而非线性关系则千变万化，不胜枚举。线性是非线性的特例，它是简单的比例关系，各部分的贡献是相互独立的；而非线性是对这种简单关系的偏离，各部分之间彼此影响，发生耦合作用，这是产生非线性问题的复杂性和多样性的根本原因。正因为如此，非线性系统中各种因素的独立性就丧失了：整体不等于部分之和，叠加原理失效，非线性方程的两个解之和不再是原方程的解。因此，对于非线性问题只能具体问题具体分析。

线性与非线性现象的区别一般还有以下特征：

（1）在运动形式上，线性现象一般表现为时空中的平滑运动，并可用性能良好的函数关系表示，而非线性现象则表现为从规则运动向不规则运动的转化和跃变；

（2）线性系统对外界影响的响应平缓、光滑，而非线性系统中参数的极微小变动，在一些关节点上，可以引起系统运动形式的定性改变。在自然界和人类社会中大量存在的相互作用都是非线性的，线性作用只不过是非线性作用在一定条件下的近似。

多指标非线性控制多指标非线性控制（Multi-index nonlinear control）是指针对非线性系统的输出函数选取为多状态量的线性组合模式的控制方法。所设计的非线性励磁控制律既能在发电机有功输出发生变化的情况下，准确维持发电机端电压在给定值上运行，又可明显地提高发电机的运行稳定性。由于该设计方案将输出函数选取为多状态量的线性组合形式，因此按此输出函数设计得到的控制律能使系统具有多指标的控制效果，即为多指标的非线性控制。

现状非线性控制方法在电力系统中的应用研究，在许多方面都取得了很大的进展，为解决电力生产的控制问题发挥了重要的作用。但在非线性控制的应用研究中尚存在着一些有待进一步研究解决的问题，如:

(1)在非线性控制设计过程中，常常难以使被控系统各状态量的动、静态性能得到满意的协调。常出现受控系统状态量的动态性能满意，但静态精度不能满足要求的情况。或是出现状态量的静态精度虽能满足要求，但状态量在受扰后的动态过程及系统的稳定性不能令人满意的问题。其原因何在是一个有待深入研究的问题。

(2)在线性控制系统的设计中，无论是线性最优控制设计，还是指定极点配置设计，都有一套方法来确定或调整系统的动、静态性能。但是在非线性控制设计中，决定系统性能指标的因素是什么，除在线性化后的系统中采用传统的控制理论外，还有没有直接在非线性控制设计中改变和调整控制系统性能的方法。

(3)线性控制设计方法的设计机理是通过调整系统的零、极点位置来达到调整系统控制性能的目的。而非线性控制设计方法的设计机理是什么，是否也是通过调整系统的零、极点位置来调整系统的控制性能。

(4)在非线性设计方法中，如何选择或确定可行有效的非线性变换，是否可寻找到一种对大部分非线性系统都具有一定普适性的输出函数形式。

分析方法对于非线性系统，建立数学模型的问题要比线性系统困难得多，至于解非线性微分方程，用其解来分析非线性系统的性能，就更加困难了。这是因为除了极特殊的情况外，多数非线性微分方程无法直接求得解析解。所以到目前为止，还没有一个成熟、通用的方法可以用来分析和设计各种不同的非线性系统，目前研究非线性系统常用的工程近似方法有：

相平面法相平面法是时域分析法在非线性系统中的推广应用，通过在相平面上绘制相轨迹，可以求出微分方程在任何初始条件下的解，所得结果比较精确和全面。但对于高于二阶的系统，需要讨论变量空间中的曲面结构，从而大大增加了工程使用的难度。故相平面法仅适用于一、二阶非线性系统的分析。

描述函数法描述函数法是一种[5]频域的分析方法，它是线性理论中的频率法在非线性系统中的推广应用，其实质是应用谐波线性化的方法，将非线性元件的特性线性化，然后用频率法的一些结论来研究非线性系统。这种方法不受系统阶次的限制，且所得结果也比较符合实际，故得到了广泛应用。

计算机求解法用模拟计算机或数字计算机直接求解非线性微分方程，对于分析和设计复杂的非线性系统，几乎是唯一有效的方法。随着计算机的广泛应用，这种方法定会有更大的发展。

应当指出，这些方法主要是解决非线性系统的“分析”问题，而且是以稳定性问题为中心展开的，非线性系统“综合”方法的研究远不如稳定性问题的成果，可以说到目前为止还没有一种简单而实用的综合方法，可以用来设计任意的非线性控制系统。

作用在对非线性控制基本原理深入理解的基础上，在长期大量深入细致的研究过程中，我们注意到如下事实:在非线性控制中，输出函数的选取决定了系统的非线性变换，从而也就决定了变换后的线性空间中状态量的构成，由此会进一步影响到非线性控制律的构成。1

因此，非线性系统中输出函数的选取应该在很大程度上影响着控制系统的性能指标，改变输出函数的形式就可以改变所设计的控制系统的性能。基于以上认识，在设计非线性励磁控制器时，我们提出了一种新的励磁控制输出函数的选取方法，将输出函数选取为发电机端电压偏差和发电机转速偏差的线性组合形式，即:

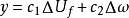
结果表明，按该方案设计的励磁控制律能很好地集AVR和PSS的功能于一身，达到了上述的设计目的。所设计的非线性励磁控制律既能在发电机有功输出发生变化的情况下，准确维持发电机端电压在给定值上运行，又可明显地提高发电机的运行稳定性。由于该设计方案将输出函数选取为多状态量的线性组合形式，因此按此输出函数设计得到的控制律能使系统具有多指标的控制效果，即称为多指标的非线性控制。

多指标约束条件下的容错控制广义系统是对实际应用中存在的一类问题比较精确的模型描述。广义系统模型存在于社会生产的诸多领域中，例如:电力系统、经济系统、机器人系统、化工过程、电网络等领域。在实际系统分析和控制系统设计中，不少实际系统，如受限机器人，反应堆，非因果系统等都只能用广义系统描述而不能用传统的系统描述。可见广义系统是描述与刻划实际系统的有力工具。因此，对广义系统的理论研究具有深远的实际意义。

近年来，连续系统的多指标约束容错控制已经取得了一定的成果，首次提出了多约束条件下的容错控制系统设计的概念，但对具体的理论和技术没有深入地研究和探讨。利用LMI方法，研究了一类线性不确定随机系统的鲁棒H。容错控制器设计方法，分析H∞。性能指标的取值范围，但其采用的故障模型简单且没有考虑极点指标和方差指标约束。研究区域极点指标与方差指标约束下的控制系统设计方法，但没有考虑故障的影响。研究一类线性不确定系统在区域极点指标、H∞指标和方差指标约束下的容错控制器的设计问题。采用连续型执行器故障模型，利用线性矩阵不等式方法，分析了相容指标的取值范围和多约束指标下的容错控制器存在的充分条件；并给出控制器的构造性设计方法。

多指标约束条件下广义系统的满意滤波近年来，在信号处理和控制工程领域，滤波理论正变得越来越重要。正常连续系统的滤波问题已经取得了一定的成果，传统的Kalman滤波理论，在形成之初，就在航天领域取得了成功的应用。在精确已知系统模型和噪声的统计特性的情况下，可以重构系统的状态，滤除噪声。因此滤波理论在状态估计和信号处理方面都取得了成功的应用。为了减少对精确模型的依赖性，使滤波理论更适合工程应用，在过去的二十年间，提高滤波算法的鲁棒性，成了人们讨论的一个重要问题。对正常连续系统的滤波问题已有很多文献提及，但是，关于广义系统的滤波问题却很少有文献提及。近年来，在工程应用中，最小方差指标、区域极点指标和H∞指标成为了控制领域和滤波领域中常用的一些指标，集中反映了估计误差的上界约束，和滤波器理想的动态性能和鲁棒性。2