[科普中国]-非线性H∞控制

背景

近年来，非线性控制越来越受到人们的重视，数学中的非线性分析、非线性泛函，物理学中的非线性动力学等，发展都很迅速。与此同时，非线性控制理论也得到了蓬勃的发展。事实上，实际系统常常是非线性的，线性仅是非线性的简化和近似。非线性控制理论的发展源自实践的需要，特别是高技术科学对精确度的要求，使得传统的线性近似方法难以解决问题。

在实际系统中，被控对象往往伴随着各种各样的不确定性，因此人们只能基于近似描述被控对象的标称数学模型来设计控制系统。所谓鲁棒性，是指系统预期的设计品质不因不确定项的存在而遭到破坏的特性。鲁棒控制对于非线性系统理论而言是一个重要的课题，而非线性H一控制理论则是解决非线性系统鲁棒控制最系统化的方法之一。

简介一种抑制外部干扰的非线性系统控制方法。这种新方法是20世纪90年代兴起的。考虑如下系统：

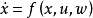
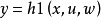
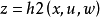
其中x是状态变量，y是量测输出变量，z是调节输出变量，w是外部信号(可以是干扰信号)，u是控制变量，f是非线性向量场，h1，h2皆为非线性向量函数.所谓非线性H∞控制问题乃是要求找到(设计)控制函数u(·)(可以是状态x的函数，也可以是量测输出y的函数)，使得在u(·)的作用下有：

1.当w=0时，闭环系统x·=f(x，u(·)，0)渐近稳定;

2.存在γ>0，使得当x(0)=0时，L2增益不等式成立，ᗄt>0.

非线性H∞控制源于20世纪80年代发展起来的线性H∞控制理论。鉴于非线性系统的多样性和复杂性，线性H∞控制的许多分析方法不易直接利用。目前主要的研究方法是利用微分对策的观点，将非线性H∞控制问题化为HJI(Hamilton-Jacobi-Isaacs)方程(或不等式)的求解问题。由于对一般非线性系统，HJI方程(不等式)的求解甚至解的存在性问题都不易解决，至今只对一些特殊的非线性系统得到较为具体的设计方法。非线性H∞控制有广泛的应用背景。

非线性控制方法回顾古典方法针对特殊系统发展了以下三种理论:

1)主要针对二阶系统发展了相平面方法性

2)针对含有一个非线性元件的高阶系统发展了描述函数法”这一近似方法;

3)针对含有一个非线性元件的系统，称为Lure系统代由李亚普诺夫理论发展出绝对稳定性理论。

李亚普诺夫方法这一方法是迄今最完善和最一般的非线性方法。正是由于这种一般性，无论用来分析稳定性或用来镇定综合，都缺乏构造性。

变结构方法严格说，变结构控制应称为具有滑动模态的变结构控制。这是20世纪50年代发展起来的一种方法，由于滑动模态具有对干扰和摄动的不变性，到80年代已逐渐受到重视。它是一种实用的非线性控制综合方法，可以赋予系统各种良好的性能和品质。但变结构控制会产生料振”，这一本质问题迄今还没有完全解决。

微分几何和微分代数方法从70年代开始发展起来的微分几何和微分代数方法，为非线性系统的控制理论找到了一种合适的工具，从而大大促进了非线性控制理论的发展，形成了从理论到应用的一次飞跃。近年发展起来的Back stepping方法等是在非线性标准形下进行的，可以看作是几何方法的间接应用。

在经历了1/ 4世纪的发展与繁荣之后，几何方法现在似乎进入了萧条时期，突破性的工作明显减少，微分几何方法的一些局限性也越来越明显地暴露出来。

非线性H∞控制理论非线性H∞控制是近年来十分热门的一个研究方向，并涉及到工程控制中的扰动衰减等问题。实际上，由于一些限制(如不确定性的种类，控制的增益等)的影响，使得在一些具体问题中对系统的不确定性难以实现干扰解祸，或用匹配及其推广条件来消除干扰，以保证系统稳定。因此，一种现实的提法是通过控制使得所需调整的输出量尽可能对干扰信号不敏感，这就是非线性H一控制扰动衰减的基本思想。

考虑如下仿射非线性系统

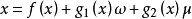
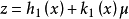
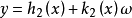
定义1、线性H∞问题是对系统寻找最小的正数ζ，设计一个控制器(如果状态可测量)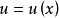 或(如果状态不能直接得到)

使得:

1)扰动衰减

2)内部稳定:当ω= o时，该控制器能使相应的闭环系统渐近稳定。

Van der Schaft等人对非线性系统H∞理论的发展做出了重要贡献。运用辛几何和动态耗散理论，给出了一种解决非线性H∞状态反馈控制的方法，即把问题归结为Hamilton Jacobi方程的可解性，这类似于线性系统H∞理论中的Riccati方程。而Hamilton Jacobi方程的解与Hamilton向量场的不变流形的存在性有关，在Hamilton系统具有一定条件及双曲平衡点的假设下，其解便与非线性系统线性化后的系统有关。

Isidoori等提出了解决非线性H∞控制问题的微分对策框架，指出了输出反馈控制器的存在与一对祸合的Hamilton Jaoobi方程的光滑正定解有关。其后，Isidoori基于对策论的框架，给出了符合分离原理的输出反馈控制器存在的条件。Lin等研究了离散非线性系统的H∞控制问题。Pavel等给出了实现非线性H∞控制的条件及控制器参数化的J 耗散描述方法。

以上都是针对确定性系统而言。对于系统不确定性的描述，通常有有界范数型、积分型、耗散型和微分包含型4种。Yang等研究了有界范数型不确定非线性系统。Nguang研究了积分型不确定非线性系统。

SOS法L2增益的控制问题，习惯上也称为非线性H∞控制。这是因为H∞范数虽是在线性系统的传递函数上定义的，不过如果转换到时域上来考虑，这H∞范数就是L2诱导范数，而在非线性系统中则称之为L2增益。L2增益的控制是指以L2增益作为系统设计时的性能指标，使之尽可能小。本文研究的是以L2增益为性能指标的非线性状态反馈律的设计。

非线性H∞控制虽然在理论上可以用Hamilton-Jacobi-Issacs ( HJI)不等式来求解，但HJI不等式目前还没有一个有效的解析求解的方法。近年来出现的SOS方法，为求解非线性H二控制问题提供了一个新的可能途径。SOS是平方和(sum ofsquares)的缩写。SOS法是指采用SOS多项式来研究非线性系统。除了对象本身的非线性特性，如果想采用高于二次型的Lyapunov函数，或者想设计高阶次的非线性控制律，就得研究一般形式的多项式。如果相应的系统的多项式可整理成SOS形式，那就一定是非负的。这个方法虽然才问世不久，但已经在一些重要的应用领域显现出了其优越性。

例如非线性系统吸引域的估计，大机动下的卫星姿态控制，飞机的姿态控制，非线性模型预测控制，时滞系统的稳定性分析，等等。在非线J险H∞控制方面也提出了一些采用SOS的设计方法。但这些方法在应用中都存在一些问题。1

非线性H∞可靠控制关于提高系统工作可靠性的理论，一直是工程控制学科的中心研究课题之一。VBillet等给出了基于Riccati方程的线性H∞理论的设计方法，使得当有控制元件失效时，闭环系统仍渐近稳定且增益有限。最近，基于非线性H∞理论，把线性系统的结果推广到非线性系统。其中，Y an等研究了具有严格冗余控制元件的非线性系统的H∞可靠控制问题，基于Hamilton-Jacobi不等式，给出了输出反馈可靠控制器的设计算法。

闭环系统是H∞可靠的，是指不仅当所有的执行机构和传感器均正常工作时，而且当有执行机构或传感器失效时，闭环系统仍渐近稳定且L2增益有限。缺点是只能有一个控制元件失效，优点是无须知道失效域。L iu等研究了不确定非线性系统的可靠控制问题，所提供的方法可以有多个控制元件失效，但是必须知道失效域。L iu等基于复制控制元件，研究了非线性系统的可靠控制问题，该方法的优点是可以有多个控制元件失效而无须知道失效域。

非线性H∞控制器的参数化通常在设计控制系统时，除了强调系统内部稳定和扰动衰减外，还有其它设计目标需要满足。解决这些复杂控制问题的方法之一是寻找控制器的集合，使得除能解决非线性H∞控制问题外，还能满足其它设计目标，因此控制器的参数化便引起人们的关注。

Isidiori等给出了一簇状态反馈控制器，但事实上需要全信息(既有状态，又有扰动)。Yung等推广的结果，基于输出反馈提供了一簇非线性H∞控制器。Lu等和A stolfi得到了一簇非线性H∞输出反馈控制器。Lu等对这一问题的处理用到了类似于线性情形的思想。A stolfi提供的方法没有给出需满足的两个输出in j ect ion main阵的明确表示，并且Hamilton Jacobi方程中涉及2n个独立变量，是状态的二倍。Yung等推广的结果，在两个需要满足的Hamilton-Jacobi不等式中只有n个独立变量，通过与渐近稳定且L2增益有限的中央控制器相联系而得到一簇控制器，证明也显得较为简单。Yang等进一步研究了状态反馈控制器的参数化问题，在该方法中不需要全信息。

非标准非线性H∞控制奇异非线性H∞控制通常是指系统中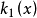 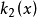， 不满秩时的控制。A stolfi研究了 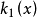不满秩的情况，运用微分同胚变换得到一个几乎处处解祸问题，进而得到实现非线性H∞控制的充分条件。Lee等研究了 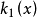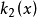，不满秩的情况，并将通常要求Hamilton Jacobi方程有正定解减弱为有半正定解。用无损分解技术研究了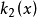不满秩的情况及控制器的降阶问题。L ink研究了非线性系统的混合控制问题。

发展需要进一步研究的几个问题2

非线性系统缺乏叠加原理这样一类线性性质，其复杂性远远超过线性系统的复杂性。线性系统研究中的一些一般性结论对非线性系统来说是不存在的，因此非线性系统的研究只能针对其自身特点寻求解决方法，才有可能得出一些具有公共性质的结论。

当前非线性H∞理论应在以下几个问题上开展深入研究：

1) Hamilton Jacobi方程已有一些近似解法，但还非常粗糙，如算法复杂，没有给出近似程度的严格分析。

2)在H∞几乎处处扰动解祸设计中，控制器的设计虽然具有构造性，但这种设计方法导致增益较高，结构复杂。

3)非线性H∞可靠控制器的参数化是一个复杂的控制问题，也是需要深入研究的实际问题。

4)在一些非线性H∞控制方法中，大都需要满足一定的光滑性条件，且控制无约束。在实际工程中，许多系统是非光滑的，且控制是有约束的。在这种情况下，应研究如何进行非线性H∞控制。

5)寻求避开目前非线性H∞控制存在的缺陷，研究全新的非线性H∞控制方法。