[科普中国]-状态空间表示

背景

现代控制面临着大而复杂的多输入多输出系统.分析这种复杂系统，必须采用一种分析和设计这种系统的新方法，即现代控制原理。这种方法要求给定系统采用简便的数学描述，从而减轻数字计算机的负担.众所周知，状态空间表示法正是系统的一种简便的数学描述和特别适合于数字计算的时间范畴表示法.因此，状态空间表示法是现代控制原理中首先要研究的一个问题。

状态空间状态空间是控制工程中的一个名词。状态是指在系统中决定系统状态的最小数目的变量的有序集合[1]。而所谓状态空间则是指该系统的全部可能状态的集合。简单来说，状态空间可以视为一个以状态变量为坐标轴的空间，因此系统的状态可以表示为此空间中的一个向量。

系统的状态空间表示法一个实际的物理系统通常以微分算子方程1

P(D)Z(t)=Q(D)u( t)

Y(t)=R(D)Z(t)+H(D)u(t) (1)

来描述。在一般控制原理中基于系统(2-1)的传递函数

W(D)=R(D)P-1(D)Q(D)+H(D) (2)

借助于各种图解法，比如根轨图或乃氏图等来实现控制系统的分析与设计。考虑到系统的相互耦合其传递函数相当复杂，有时为了简单，在定性分析中略去相互耦合，实现系统的近似分析。然而，现代控制理论是基于系统(1)的等效状态空间表示

X=AX+ Bu

Y=CX+Eu (3)

借助于数字计算机来实现系统的分析与设计，从而避免了一般控制理论中的弊病，实现了系统分析与设计的数值计算程序化。

相应于系统(3)的传递函数为

W(D)=C(DI-A)-tB+E (4)

在研究中，通常假设E=0，这样并不影响所研究的问题的实质.那末

W(D)=C(DI-A)-1B (5)

注意上面式子中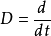， 为微分算子，P(D),R(D),Q(D)和H(D)是关于D的适当阶

次的多项式阵，Z(t)为系统的ml维部分状态，x(t)为n维状态矢量，y(t)为P维输出矢

量，u(t)为q维输入矢量,(5)式还可表示成

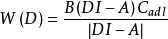
下面扼要介绍三种状态空间表示法

状态空间表达式状态空间表达式(state-space representation)由状态方程和输出方程构成，在状态空间中对控制系统作完整表述的公式。

科学解析在经典控制理论中，对一个线性定常系统，可用常微分方程或传递函数加以描述，可将某个单变量作为输出，直接和输入联系起来。实际上系统除了输出量这个变量之外，还包含有其它相互独立的变量，而微分方程或传递函数对这些内容的中间变量是不便描述的，因而不能包含系统的所有信息。显然，从能否完全揭示系统的全部运动状态来说，用微分方程或传递函数来描述一个线性定常系统有其不足之处。

在用状态空间法分析系统时，系统的动态特性是用由状态变量构成的一阶微分方程组来描述的。它能反映系统的全部独立变量的变化，从而能同时确定系统的全部内部运动状态，而且还可以方便地处理初始条件。这样，在设计控制系统时，不再只局限于输入量、输出量、误差量，为提高系统性能提供了有力的工具。加之可利用计算机进行分析设计及实时控制，因而可以应用于非线性系统、时变系统、多输入—多输出系统以及随机过程等。

方程式状态方程和输出方程总和起来，构成一个系统完整的动态描述称为系统的状态空间表达式。

在经典控制理论中，用指定某个输出量的高阶微分方程来描述系统的动态过程。

同一系统中，状态变量选取的不同，状态方程也不同。

从理论上说，并不要求状态变量在物理上一定是可以测量的量，但在工程实践上，仍以选取那些容易测量的量作为状态变量为宜，因为在最优控制中，往往需要将状态变量作为反馈量。

设单输入—单输出定常系统，其状态变量为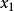 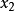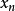， ，…， ，用矢量矩阵表示时的状态空间表达式则为：

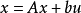
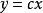
对于多输入—多输出系统状态空间表达式的矢量矩阵形式为：

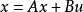
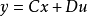
简介状态空间表示（state-space techniques ）是现代控制理论中建立在状态变量描述基础上的对控制系统分析和综合的方法。状态变量是能完全描述系统运动的一组变量。如果系统的外输入为已知，那么由这组变量的现时值就能完全确定系统在未来各时刻的运动状态。通过状态变量描述能建立系统内部状态变量与外部输入变量和输出变量之间的关系。反映状态变量与输入变量间因果关系的数学描述称为状态方程，而输出变量与状态变量和输入变量间的变换关系则由量测方程来描述。状态与状态变量描述的概念早就存在于经典动力学和其他一些领域，但将它系统地应用于控制系统的研究，则是从1960年R.E.卡尔曼发表《控制系统的一般理论》的论文开始的。状态空间法的引入促成了现代控制理论的建立。

数学基础状态空间表示的主要数学基础是线性代数。在状态空间法中，广泛用向量来表示系统的各种变量组，其中包括状态向量、输入向量和输出向量。变量的个数规定为相应向量的维数。用x表示系统的状态向量,用u和y分别表示系统的输入向量和输出向量，则系统的状态方程和量测方程可表示为如下的一般形式：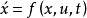

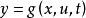
式中,f(x，u，t)和g(x，u，t)为自变量x、u、t的非线性向量函数,t为时间变量。对于线性定常系统状态方程和量测方程具有较为简单的形式：

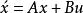
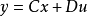
式中A为系统矩阵，B为输入矩阵，C为输出矩阵,D为直接传递矩阵，它们是由系统的结构和参数所定出的常数矩阵。在状态空间法中，控制系统的分析问题常归结为求解系统的状态方程和研究状态方程解的性质。这种分析是在状态空间中进行的。所谓状态空间就是以状态变量为坐标轴所构成的一个多维空间。状态向量随时间的变化在状态空间中形成一条轨迹。对于线性定常系统，状态轨迹主要由系统的特征值决定。系统的特征值规定为系统矩阵A的特征方程det(sI-A)=0的根，其特征可由它在s复数平面上的分布来表征。当运用状态空间法来综合控制系统时，问题就变为选择一个合适的输入向量，使得状态轨迹满足指定的性能要求。

优点状态空间表示有很多优点。由于采用矩阵表示，当状态变量、输入变量或输出变量的数目增加时，并不增加系统描述的复杂性。状态空间法是时间域方法，所以很适合于用数字电子计算机来计算。状态空间法能揭示系统内部变量和外部变量间的关系，因而有可能找出过去未被认识的系统的许多重要特性，其中能控性和能观测性尤其具有特别重要的意义。研究表明，从系统的结构角度来看，状态变量描述比经典控制理论中广为应用的输入输出描述（如传递函数）更为全面。

状态空间表示的运用对现代控制理论中其他各种方法的发展起了重要的推动作用。线性系统代数理论、线性系统几何理论和多变量频域方法，都是在状态空间法的影响下发展起来的。