[科普中国]-闭回路调整法

背景

运输问题是一类常见而且极其典型的线性规划问题。因此从理论上讲，运输问题也可用单纯形法来求解。但是由于运输问题数学模型具有特殊的结构，存在一种比单纯形法更简便的计算方法一表上作业法。表上作业法的实质仍是单纯形法。

表上作业法的计算步骤如下：

（1）用西北角规则或最小元素法确定初始基本可行解；

（2）用位势法求检验数；

（3）用闭回路调整法调整基本可行解。

基本概念基格和非基格定义1：将变量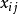 在调运表中所对应的空格记作(i，j)，称为格点(i，j)或格(i，j)。而 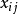的系数列向量 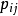也称做格点(i，j)所对应的系数列向量。若 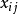为基变量，则(i，j)称为基格，否则称为非基格。

闭合回路所谓闭合回路，就是指在调运方案表中，从一个空格出发，沿水平或垂直方向前进，遇到一个适当的有数字的格子时，转90°继续前进，直到回到起始空格为止，形成一条由水平线段和垂直线段所组成的封闭折线1。

定义2：若一组格点经过适当的排序后，能写成以下形式：

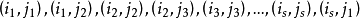
则称这组格点构成了闭合回路。

如下图中(1，1)， (1，2)，(3，2)， (3，1)构成一个闭合回路。

简介闭回路调整法是借助图表作业方式，计算比较两种（或两种以上）变量值，以调整部分经济指标实现优化经营提高管理效益的管理统计方法。

用表上作业法求解运输问题时，可仿照一般的单纯形法，检验这个解的各个非基变量（对应运输表中是的空格）的检验数是否都是正数。若有某空格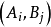 的检验数为负，说明将 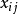变为基变量将可使目标函数值减少，即使运输费用减少，故当前这个解不是最优解。若所有空格的的检验全非负，则不管怎样变换解均不能使运输费用降低，即目标函数值已无法加以改进，这个解即是最优解。

为了计算出运输表中空格（非基变量）的检验数，引入闭回路的概念，使用闭回路可以直观地为满足约束条件换入变量增值后，再从原来的某一基变量中减去相应数值，变成数值为零的换出变量，完成换入换出即运量的调整。

示例下面举例说明闭回路调整法的计算步骤。下图是一个产销平衡的运输问题的运输表并且已使用最小元素法填入了基变量。

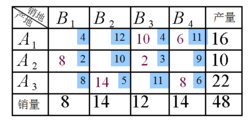
计算检验数蓝色方框中的是运价，橙色数字是基变量的值。如(A2,B1)表示从产地A2运送8个单位的货物到销地B1，其运价为2个单位。

首先考虑表中的空格(A1,B1)，设想由产地A1供应1个单位的物品给销地B1，为使运入销地B1的物品总数量不大于它的销量，就应该将产地A2运到B1的物品数量减去一个单位，即将格子(A2,B1)中填入的数字8改为7；为了使由产地A2运出的物品正好等于它的产量，且保持新的到的解仍为基可行解，需将x23由原来的2增加1，改为3。然后将x13由10减去1，即变为9，以使运入销地B3的物品数量正好等于它的销量，同时使由A1运出的物品数量正好等于它的产量。显然，由于x11的的调整将影响到x21、x23、x13这三个变量的取值，即(A1,B1)，(A2,B1)，(A2,B2)，(A1,B3)这四个格子中填入的数据。在运输表中，每一个空格都可以和一些有数字的格子用水平线段和垂直线段交替连接在一闭合回路上，而且这种闭合回路是唯一的。而且，运输问题的检验数的定义是产地到销地供给1个单位物品所引起的总运费的变化。非基变量或者说空格(A1,B1)的检验数σ11即由此引起的总运费变化是：σ11=c11-c21+c23-c13=4-2+3-4=1。可以看出在计算检验数时，符号在起点时为正，任意时针往下到下个顶点，此时符号为负，由此正负交替直到所有顶点包括进去。

检验方案的数据指标，编排各个闭合回路，这样的工作熟练可以在。现再看空格(A2,B2)，它的闭回路的顶点由以下各格组成：(A2,B2)，(A3,B2)，(A3,B4)，(A1,B4)，(A1,B3)，(A2,B3)，最后再回到(A2,B2)。

在实际操作中由于涂改不便，熟练则可以不用编制各个闭合回路，在心中假想即可，其检验数为σ22=c22-c32+c34-c14+c13-c23=10-5+6-11+4-3=1。检验数为正数，表明修改这个基变量只会增加总运费，因此观察其他空格的检验数。

按照同样的方法，可得表中其他的非基变量的检验数如下：

σ12=c12-c32+c32-c14+c13=12-5+6-11=2

σ24=c24-c14+c13-c23=9-11-5+4-3=-1

σ31=c31-c21+c23-c13+c14-c34=8-2+3-4+11-6=10

σ33=c33-c34+c14-c14+c13=11-6-11+4=12

由于σ24=-1