简介
线性规划图解法就是用几何作图的方法并求出其最优解的过程。
求解的思路是:先将约束条件加以图解,求得满足约束条件的解的集合(即可行域),然后结合目标函数的要求从可行域中找出最优解。1
基本概念可行解把满足约束条件的一组决策变量值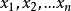 称为该线性规划问题的可行解。
称为该线性规划问题的可行解。
可行解集/可行解域满足约束条件的可行解的全体称为可行解集。
在平面上,所有可行解的点的集合称为可行解域。
最优解在可行解集中,使目标函数达到最优值的可行解称为最优解。
线性规划图解法的一般步骤1、建立数学模型。
2、绘制约束条件不等式图,做出可行解集对应的可行解域。
3、画目标函数图。
4、判断解的形式,得出结论2。
举例(1)求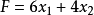 的最大值。
的最大值。
约束条件:
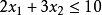
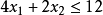
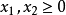
(2)绘制可行解域:
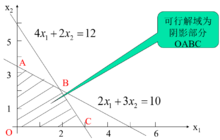
(3)画目标函数图:
令目标函数值为零,可得到斜率,根据斜率做一过原点的直线。(如果可行解域在第一象限,且目标函数等值线斜率为负)若给出问题是求最大值,把目标函数等值线平行移动到与可行解域最后相交的点,这点就是问题的最优解;若给出问题是求最小值,把目标函数等值线平行移动到与可行解域最先相交的点,这点即为问题的最优解。
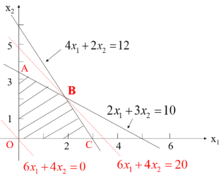
(4)判断解的形式,得出结论。
本题有唯一的最优解。
解法:
最优解是由两根直线所确定的最后的交点;
解由此两根直线相应方程所组成的方程组,得到问题的精确最优解;
将最优解代入目标函数,得最优值。
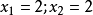
将最优解代入目标函数,得最优值:
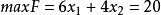




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国