[科普中国]-控制系统可观测性

简介

在许多实际问题中，控制系统的状态变量不是由直接测量得到的，而是通过某种观测方法得到的，由某种观测系统所得到的结果能否真实反映系统的状态就是系统的可观测性。

可观测性是估计理论一个专业概念，反映状态可估计性的能力。判定这种能力有两种方法：一是将问题化归为数学方程问题的求解。若数学上无解，表示此问题无解；若数学上有解，表示此问题能解；若数学上有一个解、两个解、多个解、无穷多个解，则表示该问题的解的状况。二是不将问题化为数学方程求解的形式，化为一个判定问题，只判定问题能解或不能解，这种判定形式是多种多样的。1

定义可观测性表示输出可以完全反映系统状态的特性，因此不仅要考虑系统的状态方程还要考虑输出方程。以考虑连续时间线性时变系统Σ为例，其状态方程和输出方程分别为：

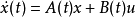
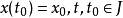
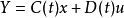
其中x为n维状态，u为p维输入，y为q维输出，t0为初始时刻。A(t)为n×n维的系统矩阵，B(t)为n×p维的输入矩阵，C(t)为q×n维的输出矩阵，D(t)为q×p维的传输矩阵，A(t)的元在J上为绝对可积，B(t)的元在J上为平方可积。

对系统的运动进行分析可知，系统Σ状态解的表达式为：

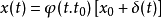
其中Φ(t，τ)为系统的状态转移矩阵，并且，如果表输入材引起的等价状态为ξ(t)

不难发现，在研究可观测性，也就是状态变量x(t)可由输出变量y(t)反映的性质时，通常输入以的等价状态孝y(t)看作是初始状态，从而可以把状态方程中U的相关项去掉。由于只考虑状态变量工(f)由输出变量y(f)的反映性，所以在输出方程中可去掉ξ(t)的相关项。

下面，基于系统的状态空间描述Σ给出状态和系统可观测性的有关定义。2

状态的不可观测性指定一个时刻t0∈J，如果存在一个时刻t1∈J另t1>t0，使连续时间线性时变系统Σ以初始状态为x(t0)=x0而的输出y(t)恒为零，即对所有的t∈【t0，t1】，y(t)=0成立，则称状态x0不可观测的。

直观上，输出y(t)对以不可观测状态而为初始状态导致的运动响应x0(t)具有?‘过滤”作用，即x0(t)不能被反映在y(t)中。可观测性表征了输出可以完全反映系统状态运动的一种特定属性。2

系统的完全可观测性指定一个初始时刻t0∈J，如果在时刻t0∈J连续时间线性时变系统Σ状态空间中所有不为零的状态都不是不可观测的，则称系统在时刻t0为完全可观测的。2

系统不完全可观测的指定一个初始时刻t0∈J，如果在时刻t0∈J连续时间线性时变系统Σ状态空间中存在一个不为零状态或者一个非空状态集合是不可观测的，称系统Σ在时刻t0∈J为不完全可观测的。

从工程实际角度来看，系统为不完全可观测是一种“奇异”状况。一个实际的系统几乎都能保证是可观测的。这就是说，即使随机地选取线性时不变系统系数矩阵A和C的元，那么几乎也能保证使系统转化为完全可观测。2

系统一致完全可观测如果在任意初始时刻t0∈J，系统Σ均为完全可观测，即系统的可观测性无关于初始时刻t0∈J的选取，则称连续时间线性时变系统Σ为一致完全可观测。

一致可观测性属于线性时变系统的特殊问题，对线性时不变系统来说，系统完全可观测一定意味着一致完全能观性。2

研究意义一个控制系统除具备调节与运算功能以外，还必须具备从生产过程获得必要的信息和向生产过程发出控制命令的功能。现在摆在设计人员面前的一个问题，就是如何知道哪些信息是必要的，哪些信息是可要可不要的?也就是哪些状态变量必须测量?这个问题正是可观测性分析要作出的回答。

可观测性分析有两个方面的意义：

1.简化检测点，以达到节省侧量仪表的目的。

2.目前尚有许多过程参数没有检测工具，在这种场合下，分析能否采用其他测量仪表代替，使许多无法检测的参数，用间接测量的办法，达到控制其状态变化的目的。3

可观侧性判断准则控制系统的可控性与可观测性分析，是现代控制理论的一个重要内容。要分析一个系统的可观测性，一般都要计算可观测性判断矩阵H。

通过对大量系统传递函数的分析，归纳六个重要准则：

1.没有分支的最简可测环节串接，由下游的状态变量可以推断上游的状态变量。

2.一个支路下游的状态变量，不能推断另一个支路的状态。

3.在同一支路里，不能由上游的状态变量推断下游的状态变量。

4.由某一状态能够推断前一个状态的条件是：关联的状态变量必须线性无关。线性无关是表示一个状态变量取定以后，可以由它唯一地决定另一个状态变量。

5.观测矩阵H的组成不应包含有与系统结构可以相约的因子。

准则5告诉我们：一个系统完全可观测，至少必须能观测最下游的状态变量。假如需要引入其他状态的观测值，组成综合观测变量，必然使观测矩阵包含有动态因子，在这种场合下，系统是否完全可控，应按准则5。

6.可观测性分析与控制作用u所加入的位置无关。这个准则已为基本定理的推导所证明，因此，在分析系统可观。测性的结构中，不应把控制作用当作支路看待。3