[科普中国]-二阶线性系统

简介

二阶线性系统（second-order linear system）简称“二阶系统”。指凡用二阶微分方程描述的系统。许多高阶系统在一定的条件下，常常近似地作为二阶系统来研究。包含有两个独立的状态变量的动态系统。可分为二阶线性负反馈系统和二阶线性正反馈系统。

二阶线性负反馈系统二阶线性负反馈系统的行为特征是寻找目标。一般分为欠阻尼形式(如图a)和过阻尼形式(如图 b)。

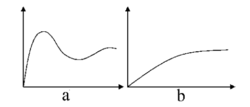
欠阻尼行为模式下，系统变量先是超过了终值，但最后则从冲过的峰值开始下降，呈减幅振荡，最终趋于 目标值。这种行为可能是由于反馈回路中过长的延迟造成，也可能是由于校正系统与系统目标之间的偏差作 用过于强烈而造成。过阻尼行为模式是单调地趋于目 标值。

二阶线性正反馈系统二阶线性正反馈系统的行为特征为趋于无穷，但呈两种不同的模式，一种是单调地趋于无穷(如图c)，另 一种是系统行为作增幅振荡(如图d)。

二阶线性系统与 一阶系统相比，最大的不同是它可能产生振荡行为，包括等幅振荡、减幅振荡和增幅振荡三种形式。

按数学模型分类二阶系统控制系统按数学模型分类时的一种形式是，用数学模型可表示为二阶线性常微分方程的系统。二阶系统的解的形式，可由对应传递函数W(s)的分母多项式P(s)来判别和划分。P(s)的一般形式为变换算子s的二次三项代数式，经标准化后可记为代数方程P(s)=0的根,可能出现四种情况:1

1.两个实根的情况,对应于两个串联的一阶系统.如果两个根都是负值,就为非周期性收敛的稳定情况.

2.当a1=0,a2>0,即一对共轭虚根的情况,将引起频率固定的等幅振荡,是系统不稳定的一种表现.

3.当a1