[科普中国]-卡方统计量

卡方统计量是指数据的分布与所选择的预期或假设分布之间的差异的度量。在1900年由英国统计学家pearson提出，是用于卡方检验中的一个统计量。

它可用于检验类别变量之间的独立性或确定关联性。例如，如果有一个按投票者性别分类的选举结果的双因子表，卡方统计量可帮助确定投票是否独立于投票者的性别，或者在投票与性别之间是否存在关联。如果与卡方统计量相关联的p值小于选定的a水平，检验将拒绝两个变量彼此独立的原假设。

也可用于确定某个统计模型是否能够充分拟合数据。例如，Logistic回归将计算卡方统计量以评估模型的拟合情况。如果与卡方统计量相关联的p值小于选定的a水平，检验将拒绝模型与数据相拟合的原假设。另一个示例是“基本统计量”菜单中的用于Poisson数据的拟合优度检验，它使用卡方统计量来确定数据是否服从Poisson分布。如果数据为离散数据，则可以报告每个类别对卡方值的贡献，从而量化每个类别差异对总卡方值有多大影响。例如，如果一个拟合优度检验拒绝了原假设，则这个结果是因为所有类别与预期稍有差异还是因为有一个类别与其预期极大不同导致的？假设您预期一盒蜡笔中包含一根蓝色、一根红色以及一根绿色的蜡笔，但实际上它包含一根蓝色和两根绿色的蜡笔，而没有红色的蜡笔。“绿色”和“红色”类别与预期不符，但“蓝色”相符。因此，“蓝色”并不影响所生成的卡方值；数据中的所有差异均来自“绿色”和“红色”类别。

卡方统计量是由统计学家皮尔逊于1900年提出的用于检验实际分布与理论分布配合程度，即配合度检验的统计量。它是由各项实际观测次数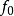（ ）与理论分布次数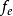（ ）之差的平方除以理论次数，然后再求和而得出的，其计算公式为：

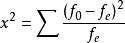
理论次数越大，该分布与卡方分布越接近，当理论次数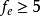 时，与卡方分布符合较好。当超过20%的理论次数小于5，或至少有一个理论次数小于1时，公式右边的表达式与卡方分布偏离较大。因此，其应用条件为至少有80%的理论次数不小于5，并且每个理论次数都不小于1。

1、卡方检验的结果与样本容量有关

对卡方检验公式稍加分析就会得出，如果总观测次数增加到原来的k倍，假如不考虑抽样误差，各类别或类别组合的观测次数所占的比例不变，则各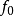 与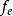 都将增加到原来的k倍，根据皮尔逊卡方统计量的计算公式，则可得出χ2值将增加为原来的k倍。而在有关检验中，卡方分布的自由度与分类指标的分类项数有关，与样本容量无关。这样，随着样本容量的增加，卡方值也将增加。然而临界值不变，这样，将会有大样本容量导致卡方检验显著的结果。实际上，除实际分布与理论分布完全一致外，即使二者存在极其微小的差异，随着样本容量的增加，都可以使得这个微小的差异达到显著的程度。

2、理论次数不符合要求时采用卡方检验

在实际应用中，卡方检验公式的适用条件为：80%以上的理论次数大于5，并且所有的理论次数不能小于1。在实际研究中，当单元格的理论数据过小时，一般采用下列几种方法进行处理：

（1）增加样本容量。如果在数据处理之前发现问题，并且补充被试可以保证测试条件不变，对研究结果没有影响，则可以补加被试，使数据符合检验要求。

（2）合并单元格。在一个分类指标为顺序变量时，如果出现理论次数过小的情况，可以调整分类项，将单元格加以合并。如学生成绩分为优、良、中、差，如果成绩为差的学生极少，使得卡方检验的条件不符合，则可以把“差”与“中”合并为“中及其以下”。

（3）取消部分单元格。当分类指标为称名变量时，若出现理论次数过小的情况，如果采用合并单元格的方法，应该合并到哪个类别及合并后类别的实际意义将不明确，这时应缩小研究范围，去除这些类别。

（4）使用连续校正（correction for continuity）公式。若四格表的理论次数大于5但小于10，这时可以根据四格表属于相关四格表还是独立四格表，采用相应的连续性校正公式计算卡方值。

（5）费舍精确概率（Fisher’s exact probability）检验法。当总数不大于20时，如果出现理论次数小于5的情况，可计算费舍精确概率进行检验1。

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趋于符合，若两个值完全相等时，卡方值就为0，表明理论值完全符合。

注意：卡方检验针对分类变量。

1、提出原假设：

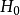：总体X的分布函数为F(x).

如果总体分布为离散型，则假设具体为：

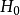：总体X的分布律为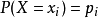， i=1，2，...

2、将总体X的取值范围分成k个互不相交的小区间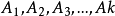，如可取

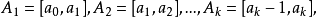
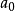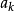其中可取，可取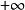，区间的划分视具体情况而定，但要使每个小区间所含的样本值个数不小于5，而区间个数k不要太大也不要太小。

3、把落入第i个小区间的Ai的样本值的个数记作fi，成为组频数（真实值），所有组频数之和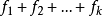等于样本容量n。

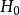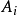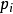4、当为真时，根据所假设的总体理论分布，可算出总体X的值落入第i 个小区间的概率，于是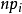，就是落入第i个小区间Ai的样本值的理论频数（理论值）。

5、当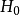为真时，n次试验中样本值落入第i 个小区间Ai的频率与概率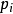应很接近，当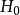不真时，则相差很大。检验卡方统计量，在0假设成立的情况下服从自由度为k-1的卡方分布。