有向程序流程图是指用于分析程序运行过程或执行功能的有向图。有向程序流程图是软件设计中常用一种图,它能让软件设计人员更好设计软件功能和修改软件的不足。有向程序流程图一般可以用过UML语言来实现。前趋图就是一种有向程序流程图。
程序流程图当程序中有较多循环语句和转移语句时,程序的结构将比较复杂,给程序设计与阅读造成困难。程序流程图也叫程序框图,它用图的形式画出程序流向,使人们能够直观而且清楚地看到程序结构,流程图由框和带箭头的线组成,箭头指示程序流向。框又分为两种,一种为方框(矩形框),框内标明对应程序段应完成的任务,另一种为菱形框或椭圆形框,有两个以上的出口,称为分支框,框内记载分支条件。常用的框图中有四种图示: 用矩形表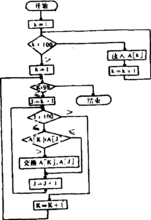 示处理框,表示某种运算或处理有一个入口一个出口。用菱形表示判断框,用以检查和判断某些待判定的问题,通常它有一个入口,二个出口。表明有两种可能选择,而判断结果只选择其中之一。两端为半圆形而上下两边为两条平行线组成的复形框,称起止框,用以表示过程的开始或终结。带箭头的方向线,称流程线,表示流程图的路线和方向。例如,要求编程实现从键盘读入100个数, 并按从小到大的次序把它们存入一个数组中, 程序流程图见图。程序如下:
示处理框,表示某种运算或处理有一个入口一个出口。用菱形表示判断框,用以检查和判断某些待判定的问题,通常它有一个入口,二个出口。表明有两种可能选择,而判断结果只选择其中之一。两端为半圆形而上下两边为两条平行线组成的复形框,称起止框,用以表示过程的开始或终结。带箭头的方向线,称流程线,表示流程图的路线和方向。例如,要求编程实现从键盘读入100个数, 并按从小到大的次序把它们存入一个数组中, 程序流程图见图。程序如下:
程序流程图能直观、清楚地表现程序,因而给程序的编写和阅读带来很大的方便。同时流程图可以看作算法的形象化描述,它独立于编程语言,有很好的通用性。编程之前应该先画程序流程图,养成良好的编程习惯。
前趋图前趋图(Precedence Graph)是一个有向无循环图,记为 DAG(Directed Acyclic Graph),用于描述进程之间执行的前后关系。图中的每个结点可用于描述一个程序段或进程,乃至一条语句; 结点间的有向边则用于表示两个结点之间存在的偏序(Partial Order, 亦称偏序关系)或前趋关系(Precedence Relation)“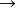 ” 。
” 。
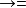 {(
{( )是指步骤
)是指步骤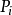 必须在步骤
必须在步骤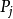 开始之前完成,如果(
开始之前完成,如果(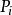 ,
,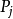 )
) ,可写成
,可写成 →
→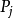 ,称
,称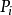 是
是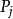 的直接前趋,而称
的直接前趋,而称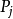 是
是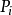 的直接后继。在前趋图中,把没有前趋的结点称为初始结点(Initial Node),把没有后继的结点称为终止结点(Final Node)。此外,每个结点还具有一个重量(Weight),用于表示该结点所含有的程序量或结点的执行时间。
的直接后继。在前趋图中,把没有前趋的结点称为初始结点(Initial Node),把没有后继的结点称为终止结点(Final Node)。此外,每个结点还具有一个重量(Weight),用于表示该结点所含有的程序量或结点的执行时间。
图 G 的边的两个顶点是无序的,一般称为无向图,在实际应用中,将图和每条边分配一个方向是很自然的,给图 G 的每一条边规定一个方向,则称其为有向图。对有向图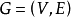 ,有向边 e 用与其关联的顶点 u , v 的有序对来表示,即
,有向边 e 用与其关联的顶点 u , v 的有序对来表示,即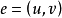 表示 u 为边e 的起点,v 为边e的终点1。
表示 u 为边e 的起点,v 为边e的终点1。
统一建模语言(UML)是一个通用的可视化建模语言,用于对软件进行描述、可视化处理、构造和建立软件系统制品的文档。它记录了对必须构造的系统的决定和理解,可用于对系统的理解、设计、浏览、配置、维护和信息控制。 UML 适用于各种软件开发方法、软件生命周期的各个阶段、各种应用领域以及各种开发工具,是一种总结了以往建模技术的经验并吸收当今优秀成果的标准建模方法。 UML包括概念的语义,表示法和说明,提供了静态、动态、系统环境及组织结构的模型。它可被交互的可视化建模工具所支持,这些工具提供了代码生成器和报表生成器。 UML标准并没有定义一种标准的开发过程,但它适用于迭代式的开发过程。它是为支持大部分现存的面向对象开发过程而设计的。
UML描述了一个系统的静态结构和动态行为。 UML将系统描述为一些离散的相互作用的对象并最终为外部用户提供一定功能的模型结构。静态结构定义了系统中重要对象的属性和操作以及这些对象之间的相互关系。动态行为定义了对象的时间特性和对象为完成目标而相互进行通信的机制。从不同但相互联系的角度对系统建立的模型可用于不同的目的。U M L还包括可将模型分解成包的结构组件,以便于软件小组将大的系统分解成易于处理的块结构,并理解和控制各个包之间的依赖关系,在复杂的开发环境中管理模型单元。它还包括用于显示系统实现和组织运行的组件。
应用利用有向图判别磁共振成像射频线圈的设计流程图
为了简化对判别方法的应用,我们把判别过程分为3 步。步骤1,将程序流程图抽象成有向图; 步骤 2,观察有向图,看它是否符合图论第一基本定理,如果符合,继续步骤 3,否则流程图有逻辑性错误;步骤 3,观察此有向图,无论从哪个顶点( 不包含结束点)出发,沿箭头方向是否均可以走到结束点,如不能则存在死循环,即死锁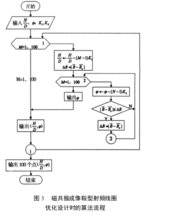 现象,可判定流程图错误。磁共振成像( MRI)是当前医学界最先进的诊断技术,广泛应用于临床,MRI 在成像过程中,射频场的均匀性是决定 MRI 性能的重要指标,射频必须在扫描区内产生均匀的发射磁场,使线圈在共振频率处的Q 值很高才能获得清晰的图像,所以,射频线圈的优化性尤其重要 。图为磁共振成像鞍型射频线圈的优化设计流程图,此流程图是用于计算磁通量关系曲线的框图,是为试验提供均匀磁场的条件算法流程图。
现象,可判定流程图错误。磁共振成像( MRI)是当前医学界最先进的诊断技术,广泛应用于临床,MRI 在成像过程中,射频场的均匀性是决定 MRI 性能的重要指标,射频必须在扫描区内产生均匀的发射磁场,使线圈在共振频率处的Q 值很高才能获得清晰的图像,所以,射频线圈的优化性尤其重要 。图为磁共振成像鞍型射频线圈的优化设计流程图,此流程图是用于计算磁通量关系曲线的框图,是为试验提供均匀磁场的条件算法流程图。
按优化步骤对实际问题进行判别,可以看到,此流程图结构复杂,在没有进行程序测试之前,很难直观判别它的逻辑性和优化性,按照图论的方法,根据步骤1,首先把流程图抽象成有向图,为了看起来方便 ,我们把抽象成有向图的黑点用 ①②③…这种序号来表示,如图所示1。
根据步骤2,由图论第一基本定理,对于图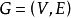 ,恒有∑
,恒有∑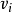 ∈
∈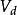 (
(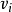 )=2| E |,即每个顶点的度数之和=2*总边数之和。从图 4可以直观地看出,顶点①的度数依次为 1,2,4, 2,5,2, 2,3, 2,4,2, 1,总和为30,总边数为15,该
)=2| E |,即每个顶点的度数之和=2*总边数之和。从图 4可以直观地看出,顶点①的度数依次为 1,2,4, 2,5,2, 2,3, 2,4,2, 1,总和为30,总边数为15,该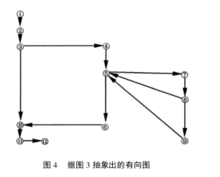 有向图满足图论第一定理,流程图逻辑性正确。根据步骤 3,可以看到,无论从有向图的那个顶点出发 ,都可以沿着箭头的方向到达终点,例如:⑤
有向图满足图论第一定理,流程图逻辑性正确。根据步骤 3,可以看到,无论从有向图的那个顶点出发 ,都可以沿着箭头的方向到达终点,例如:⑤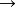 ⑦
⑦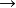 ⑧
⑧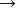 ⑨
⑨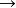 ⑤
⑤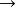 ⑥
⑥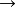 ⑩,说明该设计不存在死循环。
⑩,说明该设计不存在死循环。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国