[科普中国]-盆地流体模拟

背景

盆地流体流动是盆地动力学背景、构造、沉积充填、热史综合作用的结果(Garven，1989，1995)。盆地流体模拟的目的就是要再现盆地演化过程中流体活动规律，包括盆地演化过程中沉积物物性、温度场、压力场以及流体流动速度、流量、水 -岩相互作用速率等参数随时间的变化(Bethke等，2001)，进而可为盆地内油气运移和聚集、成矿流体运移和聚集提供依据。因此，盆地流体模拟是成矿流体或油气运聚模拟的基础(康永尚等，1999;解习农等，2003)，也是盆地内地质资源评价中必不可少的一个环节。1

盆地流体活动的基本原理盆地流体活动虽然错综复杂，但它总是遵循两条基本原理，即流体活动过程中的质量守恒和 能量守恒定律。下面介绍盆地流 体模拟过程所 遵循的基 本原理。

(一)达西定律

法国工程师 H.Darcy在 1856年发表了水通过直立均质砂粒渗滤管的实验结果，结果表明流体渗滤速度总是与测压管水柱高差和渗流系数成正比，即：

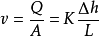
式中，v为流体渗流速度(cm/s);Q为单位时间内流体渗滤过滤管的体积量，或流量(cm3 /s);A为管道横截面积(cm2 );Δh为测压管水柱高差(cm);Δh/L为水力梯度(cm/cm);K为水力传导系数，即渗流系数。

（二）质量守恒定律

当流体通过孔隙介质内一个截面时，在任一时间间隔内从这个截面流出的质量等于向这个截面流入的质量，即所谓连续性方程。

（三）溶解物质质量守恒定律

盆地流体分子浓度扩散可表述为：

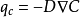
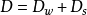
式中，D为扩散系数;Dw 为水动力热扩散系数;Ds 为分子扩散系数;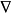 C为浓度差。

基本模型盆地流体流动过程既包括水动力过程，也包括热传导过程和溶质运移过程：

1.水动力模型

根据达西定律，盆地流体流动受压力差的驱动，单位体积的流速可表述为：

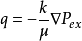
Pex是剩余孔隙压力，即流体压力与静水压力之差。

2.热动力模型

盆地流体流动过程扩散既包括随流热扩散和岩石热传导，有时还有新生热源，如由放射性元素所产生的单位体积的产热量，表达式为：

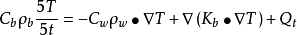
式中：Cb为骨架岩石的特征热;Cw 为孔隙流体的特征热;Kb 为骨架岩石的热传导系数;Qt 是由放射性元素所产生的单位体积的产热量。

3.溶质运移模型

盆地流体中化学物质运移既包括水动力扩散，也包括由分子振动使物质从高浓度向低浓度的扩散作用，其表达式为：

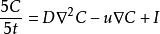
式中：u为流体的孔隙 平均流速(m/L);D为水动力弥散系数 m2/L;D=D″+D′，D′为机械弥散系数，D′=αu，α为弥散度(dispersivity)，D″为多孔介质分子扩散系数;I为源汇项。1

基本方法盆地流体模拟的方法有两种：一种是用解析方法，另一种是数值方法。前者就是用数学上的积分法或积分变换等方法直接求数学模型的解，它是数学模型的精确解；后者则是用离散化的方法求解数学模型，其解为数值的集合，是数学模型的近似解。在盆地流体模拟中，由于流体活动发生于一个非均质的复杂地层系统之中，用解析方法必须对于研究对象做出各种假设条件，例如假设地层是均质的，边界是简单的几何形状等等，这种解析解的结果可以简单明了的看出盆地流体运动的一般规律。然而，沉积盆地是十分复杂的，用解析方法所做的一些简单假设不能完全反映地层的真实情况，如各向异性、特殊边界情况、盆地演化过程中的不规律性变化现象等。使用数值方法求解数学模型，恰好弥补了解析方法的不足，它通常是将研究范围离散化，也就是进行网格剖分，然后将模拟区域的网格方程联合求解，进而得出数值解的集合（陈崇希等，1990）。因此，数值方法成为盆地流体定量模拟中最重要的方法。

数值方法求解数学模型的方法有两种，一种是有限差分法，另一种方法是有限元法。这两种方法最大区别在于有限元法可以更好地模拟复杂的边界条件，用各种形状（一般为三角形）的网格单元最大可能地逼近模拟边界，所以一般用于那些边界影响比较大的问题的求解；而有限差分法可以很顺利地建立差分方程，在精度允许的范围内采用简单的网格系统将模拟区域离散化，此外有限差分法的求解更为简单一些。1

应用分析盆地流体模拟的应用已在国内外有许多报道，许多学者都试图从盆地水动力学过程来探讨盆地流体活动与油气运移、聚集 的成因联系(Ungereretal.，1990;Bethkeetal.，1991;Gvirtzman& Stanislavsky，2000;Lee& Williams，2000;Xieetal.，2001，2003)。盆地流体既是油气运移、聚集的载体，也是其他成矿流体的载体，所模拟的古水动力场及演化特征可以作为其他模拟研究的基础，比如油气成藏动力学模拟、与地下水活动相关的生物作用过程模拟等。下面以松辽盆地十屋断陷的实例模拟作一介绍。

(一)模型参数的获取

盆地流体数值模拟方法需要地质、地球物理、地球化学、热力学、岩石物理学以及流体力学等多方面的各种参数，这些参数的正确选取直接关系到模拟结果的可信度。这些模型参数包括地质参数、岩石物理学参数和流体力学参数。

地质参数包括沉积地层地质年代、厚度、岩性、古水深、古地表温度、古热流、地温梯度、沉积相以及盆地演化过程中的地质事件等内容。有些参数可以通过钻井、地震资料和测试资料获取。

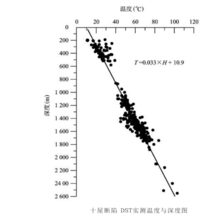
需要说明的是盆地演化过程中古地温和地温梯度可能是变化的，因此在盆地流体模拟中需要获取不同地质时期的古地表温度和古地温梯度。比如，在十屋断陷实例的模拟中就采用了不同的地热资料，即裂陷期的古热流值为 2.9HFU，裂后期为 1.95HFU，现今热流值为 1.55HFU。岩石物理学参数包括密度、孔隙度、渗透率及其压缩系数、热导率、热容(即比热)和热膨胀系数等。

流体力学参数主要包括流体密度、黏度、压缩系数与膨胀系数、饱和度、溶解度、体积系数以及气体扩散系数等。多数流体力学参数如流体密度、黏度、溶解度等随温度和压力的变化而变化。

(二)模拟结果分析

选择通过十屋断陷的 NE向剖面，通过数值模拟揭示了盆地演化过程中温度场、压力场和流体流速等变化情况。模拟结果与钻井实测的温度和 Ro 具有很好的吻合关系。

模拟结果表明：十屋断陷地层压力体系经历了从异常高压向异常低压的演变过程。营城子组沉积期末在断陷中央已出现异常高压，至登娄库组沉积期末，异常压力变大，其范围也变大。该区异常高压形成可能与裂陷期快速沉降速率有关，凹陷中央沙河子组和营城子组沉积速率达 200m/Ma以上。进入裂后期，由于沉积速率较低，一般小于 100m/Ma，至晚白垩世青山口组、姚家组和嫩江组沉积期其沉积速率小于 50m/Ma，断陷内异常超压减小，但仍表现为高的剩余压力。直到进入新生代地层抬升剥蚀期，地层压力逐渐从异常高压转变为异常低压。1