[科普中国]-决策关键线路法

概述

关键路线法和计划评审技术已为各行各业各部门广泛采用，成为计划管理的有力工具。但是这些方法主要着 眼于时间，总是从工期上进行分析和计算，尽量做到按规定工期或在尽可能短的时间内完成。在网络图中没有反 映资源（人力、物力）和成本，而这些却又是工程规划中必须考虑的，这就需要进一步研究时间——资源和时间——成本问题。
每项活动需要多种资源，它们之间存在一种最优配置，那么各种资源的消耗也可以用成本来反映。考虑到有些活动由于采用了不同的技术、不同的资源（也可以是同种资源数量上的增减）或不同的组织方式，需要的成本不同，完成的工期也不同，这就产生了不同的方案。有时为了缩短某项活动的工期动用了某种紧张的资源或增加 了某种紧张资源的数量，我们也可以大大提高该资源消耗所反映的那部分成本，从而间接地反映出资源的约因此 ，我们着重分析时间成本问题。
在上面所讲到的不同方案中，我们总是希望选择在下面两种意义中的一种最优方案工期一定而成本最低；成本一定而工期最短。为了解决这一问题，近年来发展了考虑成本与工期关系的网络计划法，先找到成本与工期的近似函数关系，然后用数学规划的思想和方法找出最优解。这种方法由于成本与工期的函数关系较难获得而没有得到很大的推广。
在工程实践中，某些活动可供选择的方案成本与工期不同数目常常是有限的，而需要作出决策的场合也是有限的。不需要处理复杂的函数关系。
举例来说，在制造混凝土预制件时，对浇灌后的构件在拆模前可以浇水养生，经过较长时间后方能拆模。在浇灌后也可以采用蒸汽养生的方法，迅速提高早期强度，拆模。因此拆模前的养生采用浇水和蒸汽养生两种，前者的时间长成本低，后者却相反。再如，需要某设备或部件，可以采用本单位加工和外协的方法。在本单位加工 虽然成本较低，但在能力有限或加工任务趋于饱和时加工周期长。如委托外单位加工，时间虽短但成本较高。以上两个例子都说明，在某一项活动中，只有有限个两、三个或再多一点可供选择的方案，而且在整个工程中，也只有为数不多的几个活动有这种选择余地。

在编制网络图时怎样反映这种可供选择的情况呢？一种方法是针对每种情况画一张网络图，作为一种方案，然后进行分析比较，这样做不胜其繁。另一种方法就是近年来有人提出的决策关键线路法(简称DCPM) ,这种方法的特点是在一般的网络图(采用单代号网络图)上增加一些决策点,表明在这些活动上有不同的方案可供选择。一个 网络图可以有多个决策点，反映出有多个需要作出选择的活动。每个决策点上有几个可供选择的方案（每个方案 工期、成本都不同），由拟订计划的人全面地根据工期、成本加以分析，选择合理的实施方案。

DCPM除了能在任务开始前进行决策外，也可以在执行过程中采用。由于某种原因，有几项活动耽误了时间，影响了整个工期。此时开始认为合理的方案就不一定是合理的了。因此在可能的情况下，可以根据此刻的条件重新进行决策，来选择新情况下的合理方案。
因此，DCPM与CPM相比，它可以提供多种可能来供领导进行决策时使用，不象CPM只是一种可能。

DCPM比较适合于我们在工作中进行比较决策用，特别适合供领导进行决策和使用1。

DCPM的表示法令任务

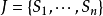
为1到n项活动之集合，活动Si在单代号网络图中可以用节点O表示。活动间的逻辑关系可以用节点间的带箭线段表示。
这样，网络图就是集合J和在J上定义的先行关系。
在DCPM中，除了那些必须完成的活动外，某些活动是若干项互斥活动的集合。这些活动可以表示为

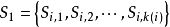这些互斥活动中有一项完成了就标志着该决策活动的完成。在单代号网络图中用下图表示。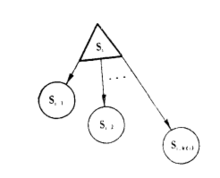同样可
以用带箭头的线段表示活动间的关系。我们采用决策变量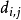 来表示活动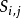 的完成与否。若活动 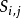必须完成，则 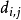为1，若活动 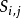不去完成，则 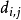为0。

因此，DCPM的网络图就是集合J和J上定义的先行关系及决策活动上定义的互斥关系。

在DCPM的网络图中由于决策活动中活动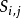 的互斥性，其中一些活动是 要完成的，而另一些活动就不必完成。这些不完成的活动在网络图中将消失，与这些活动有关的紧前、紧后关系也将随之消失，为了保证网络图中先行系统的正确性，我们必须考虑到：（1）如果 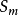只有唯一的紧前活动 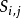,就必须在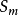 的紧前活动中增加一个 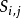的紧前活动。这样可以避免一旦 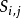消 失后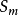， 失去唯一的紧前活动。（2）同样当 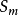有唯一的紧后活动 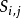, 也必须在 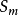的紧后活动中增加一个 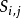的紧后活动。（3）如果两个活动是由 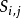连结起来的，虽然它们具有多个紧前活动和紧后活动，为了在 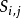消失的情况下仍能保持两者间的逻辑关系，也需增加一个关系。 三种情况的网络图如图中的a，b，c1。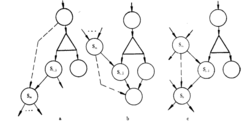

DCPM的改进算法原网络图是用单代号表示，但是我国广大工程技术人员所熟悉的CPM和PERT网络图大都是双代号表示的，DCPM与CPM及PERT存在着密切的联系，为了便于应用，我们把单代号DCPM网络图改用双代号表示。
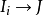双代号DCPM网络图采用了双代号CPM及PERT的网络结构，并在此基础上增加决策工序，其表示形式见图1-1。这里，I表示以决策点为始点的决策工序；表示决策工序（I,J）的第i个选择第j个方案,决策工序中的虚箭线只起逻辑联系作用，没有其它含意。

下图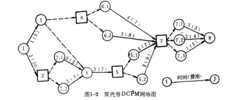1-2为一个具有4个决策工序和5个非决策工序的双代号网络图。

在双代号网络图中，一个决策点只能表示一个，且仅仅一个决策工序的开始，不能有两个或多个工序的始点为同一决策点，但是可以有两个或多个工序的终点为同一决策点，在双代号网络图中允许有虚工序存在，应注意和决策工序中的虚箭线的区别2。