BP 神经网络具有一定的非线性逼近能力,但存在着固有的缺陷,如:学习收敛速度慢,中间隐层节点数的选择无规律,易于陷入计算能量局部极小,因而只能用于粗略回归,难以实现精确拟合,且不易由硬件实现。而函数链神经网络通过对输入的函数扩展,将多层网络缩为单层网络,使该网络具有极强的非线性映射能力,达到了快速、高效的学习目的,避免了陷于局部最小的问题,从而成为一个应用极广的神经网络模型。
函数链神经网络具有很强的映射功能,能构造出任意复杂的连续函数。其基本思想是通过采用一组线性无关(或正交)函数将原输入样本扩展模式矢量,在维数更高的空间上对模式进行表示和区分,得到了在增强的空间里多个独立的新输入样本,将其再输入到单层前向网络。函数扩展采用模式识别的思想,在没有引入新的信息条件下,将低维模式变换到高维模式,增强了模式的表达,使原来在低维空间中的非线性问题在高维空间中得到解决。由于增加了扩展过程,函数链神经网络能实现多层感知机的功能;同时,在学习中仅为单层运算,故其收敛速度极快,且不会陷入局部最小,因此,能用于精确估计和拟合。
函数链神经网络在结构上由函数扩展和单层感知器 2 部分组成,分别如图 1 和图 2 所示。对函数扩展部分进行某种非线性变换,由此将每一输入分量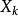 变换为一系列线性独立函数
变换为一系列线性独立函数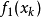 ,
,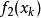 ,…,
,…,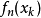 ,从而将模式矢量的空间维数变为独立函数的高空间维数,这样,新的信息表述空间被扩展,使单层网络具有了分辨复杂对象的能力。1
,从而将模式矢量的空间维数变为独立函数的高空间维数,这样,新的信息表述空间被扩展,使单层网络具有了分辨复杂对象的能力。1
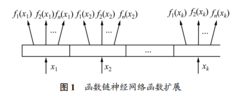

函数链神经网络是一种引入非线性扩展函数的单层网络, 具有很好的非线性逼近能力, 在其输入端使用线性无关的增强模式表达, 用单层网络可以形成各种超平面函数, 不需要广义的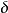 规则训练网络, 只用简单的
规则训练网络, 只用简单的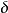 规则或一般的递推方法就可以收敛,不仅学习速率高, 而且简化了网络结构和学习算法, 其拓扑结构如图1所示。2
规则或一般的递推方法就可以收敛,不仅学习速率高, 而且简化了网络结构和学习算法, 其拓扑结构如图1所示。2
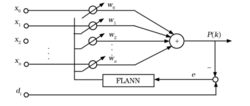
设有 个输入
个输入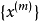 ,
,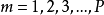 ,每个输入样本
,每个输入样本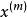 经函数扩展后产生
经函数扩展后产生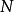 个分量分别为:
个分量分别为:
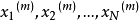 ,每个单一元素产生一个输出
,每个单一元素产生一个输出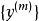 ,
,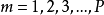 , 沿着连接的加权因子
, 沿着连接的加权因子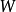 ,对应的输入输出表达式为:2
,对应的输入输出表达式为:2
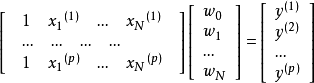 即:
即:
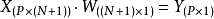 因此,网络输出
因此,网络输出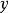 的问题变为求解权系数
的问题变为求解权系数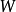 的问题。
的问题。
(1)当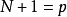 时,扩展函数的个数加一与输入样本个数相等,此时,由于扩展函数均选为正交或线
时,扩展函数的个数加一与输入样本个数相等,此时,由于扩展函数均选为正交或线
性无关的函数,所以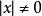 , 可得
, 可得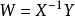 , 权系数
, 权系数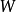 为一个严格的平面网络解;
为一个严格的平面网络解;
(2)当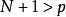 时, 先把
时, 先把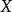 矩阵分块, 得到分块阵
矩阵分块, 得到分块阵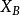 ,其维数为
,其维数为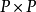 , 且
, 且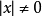 , 设置
, 设置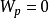 , 使得
, 使得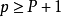 ,可得
,可得 ;
;
(3)当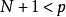 时,可以得到解:
时,可以得到解: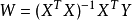 。
。
函数的扩展总是通过产生一个平面网络的解法,使用 FLANN 和自适应监督学习算法来完成。对于实际数据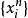 ,
,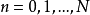 作为 FLANN 的输入,进行神经网络算法之前, 先对实验数据标定, 标定点要分布在整个测量范围之内, 同时为保证学习过程收敛,对数据进行归一化处理。
作为 FLANN 的输入,进行神经网络算法之前, 先对实验数据标定, 标定点要分布在整个测量范围之内, 同时为保证学习过程收敛,对数据进行归一化处理。
构成以下算法:
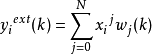
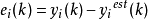
权值调整算法为:
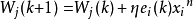 式中,
式中,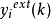 ,
,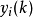 ,
,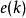 ,
,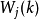 分别代表估计输出、期望输出、误差和函数链神经网络在第
分别代表估计输出、期望输出、误差和函数链神经网络在第 步的第
步的第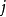 个连接权值;
个连接权值;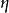 为表示一个控制稳定性和收敛速率的学习因子。
为表示一个控制稳定性和收敛速率的学习因子。
函数链神经网络的输出值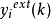 与第
与第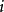 个实际值进行比较, 经函数链神经网络学习, 求出函数链神经网络的输出估计值与第
个实际值进行比较, 经函数链神经网络学习, 求出函数链神经网络的输出估计值与第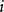 个实际值均方差在全局范围内达到最小。
个实际值均方差在全局范围内达到最小。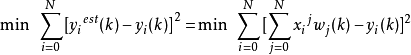 求得的最小值是关于权值
求得的最小值是关于权值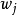 的函数
的函数




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国