[科普中国]-鲁棒最优控制

简介

鲁棒最优控制是在60年代发展起来的一种设计方法，它以状态空间描述的线性系统为对象，以状态变量和控制变量的二次型函数的积分为目标，得到的反馈控制律可以实现最优控制。由于这种方法计算容易，控制效果明显，所以应用范围十分广泛。近年来，H∞控制理论得到了很大发展，理论也不断得到完善，研究的对象主要针对含有建模不确定性等因素造成参数摄动的系统，设计得到的控制器具有鲁棒性好的特点，应用前景良好。1

发展历史控制科学从产生、发展到辉煌，几乎贯穿了整个20世纪。对它的研究从一开始就表现出与研究其他自然科学(例如物理学)不同的特点。少受干扰与纯粹化是自然科学中研究基本原理的准则。控制科学由于其目的是针对现实解决问题的，因此从它一产生起就必须不断地考虑干扰和非纯粹化的影响，而且，在不同阶段不同条件下这种考虑有其不同表现。

控制科学中最重要的一个概念就是反馈，而反馈的最主要之点就在于考虑了实际系统中存在的不确定性。人们发现，当反馈不再限于常数增益而是动态系统时，反馈在闭环系统动力学中十分重要。在一定程度上它可使闭环系统具有合适的动态特征而不受开环所可能产生的摄动影响。这一点能奏效的原因之一是系统简单。

随着控制系统应用范围的扩大，对象的日益复杂，系统与环境均充满不确定性以及更为严格的控制要求，使我们正面对一个系统复杂程度日益增大和控制要求日益提高的充满挑战的时代。而控制系统复杂性中不确定性是最重要的一个因素。大量数学工具从应用角度引入控制研究和计算机技术的飞速发展为迎接这个挑战创造了条件。这就是20世纪80年代出现的鲁棒控制飞速发展的前提。

G．Zames在1981年发表的著名论文，可以看成是现代鲁棒控制特别是H∞控制的先驱。它以最优敏感性，即干扰在输出上影响最小作为H∞控制的基本提法。这实际上是Wiener—Hopf理论和二次型最优控制的发展。但随后的研究发现，这种H∞最优控制的求解实际上可以解决一系列鲁棒控制问题。这表明鲁棒控制与最优控制具有某种深刻联系。

H∞控制中一个具有里程碑性质的结果是J．C．Doyle等四人的著名文章。他们将H∞问题的求解归结为求解两个Riccati方程，从而沟通了二次型最优控制与H∞控制的本质联系。如同绝对稳定性问题的研究中Popov频域方法与Lyapunov函数的时域方法得到沟通时出现的学术繁荣场面一样，这一新的突破性的联系就使得H∞的研究获得了新的推动力，使在理论上和计算上均取得了极大的发展，从而使线性H∞控制的研究在几年里就取得成功并达到基本完善。

随后，周克敏博士所著《RobustandOptimalControl》，正是适应这个形势需要，及时地对线性鲁棒与最优控制，特别是对H∞控制进行了总结提炼并系统化，使其成为这个领域最早的高水平的理论著作。2

鲁棒性(Robustness)无论是对于何种形式的预测控制算法，鲁棒性研究一直是其理论研究中的薄弱环节。实际工业过程存在于不确定性环境，总会受到预先未知的各种不确定性的影响；模型和被控对象之间也不可避免地存在着失配。基于模型设计的最优控制律应用于实际对象可能导致系统性能变差，因此研究MPC鲁棒性是十分必要且有实际意义的。总的来说，MPC鲁棒性问题的研究分鲁棒分析和鲁棒综合两个方面。3

MPC鲁棒性分析Garcia和Morari于80年代初提出在IMC框架下研究MPC性能，并简单分析了MPC系统的鲁棒性，推导了预测控制在内模控制结构下的定量表达，然后由模型和对象之间的失配来分析鲁棒性，其优点是可以定量地研究设计参数与系统鲁棒性间的关系，但较局限。在上述基础上，又研究了一类MPC系统在模型增益失配和时滞失配时的鲁棒性，给出了增益和时滞的允许失配范围，以及失配度变化趋势和系统鲁棒稳定性的关系，但所得定理只是充分的，且仅针对这一类系统。随后，以对象到闭环系统特征多项式的系数映射为基础，分析了CARIMA模型中噪声滤波器T对于闭环系统鲁棒性的影响，并通过比较得出GPC中噪声滤波器T作为设计参数时，其地位实际上相当于DMC中的校正参数，它们都对模型失配时的闭环系统鲁棒性产生很大影响。3

MPC鲁棒综合鲁棒综合问题是建立在被控对象模型不确定性描述基础上的。大多数鲁棒MPC设计都基于min-max描述，具有H∞控制的思想，即将MPC的在线min优化问题变为min-max优化，求解控制律使在不确定性最坏情况(worstcase)下的目标函数值最小。根据目标函数和不确定性描述的不同，可将鲁棒MPC设计分为如下三类：

1)基于不确定FIR模型的min-max设计。

2)基于LMI的MPC。

3)滚动时域H∞控制。3

鲁棒最优控制器结构及原理鲁棒控制理论保证了系统在参数摄动和外加干扰情况下具有闭环稳定性，但是对于随动系统而言，良好的跟随特性是必须的要求，为了达到满意的效果，得到如图所示的控制结构。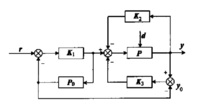

在图所示结构中，P为对象的实际模型，设P0s为P的数学模型，即标称对象，P0为P的标称对象P0s与控制器K2形成的闭环，d为外加干扰，K1、K2、K3为控制器，输入为r，输出为y0。

对上述控制结构的解释如下：由于对象的实际模型可能存在一定的参数摄动，并且对象本身可能受到外部干扰，引入鲁棒控制器K2就是为了增强系统的鲁棒性，抑制干扰，降低系统对对象参数摄动的敏感度；K1为最优控制器，它根据P0进行设计，目的是满足系统的跟随特性；控制器K3的作用是消除实际系统输出y与标称系统输出y0之间的误差，当P=P0s，即实际对象与标称对象一致的时候，有y=y0；当P≠P0s时，y与y0就不相同，可以通过控制器K3的调节使得y与y0达到一致。1

控制器设计最优控制器K1的设计由如下定理给出。设系统输出的期望值为y0，二次型性能指标为

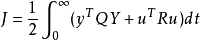
则最优控制器为

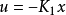
其中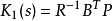

P为Riccati方程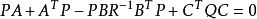的解

控制器K3的参数可以通过仿真得到，调节的标准是使得实际对象与标称对象输出之间的误差衰减具有良好的动态特性。1

机器人的鲁棒最优控制结构机器人单通道速度控制系统的鲁棒最优控制结构如图所示。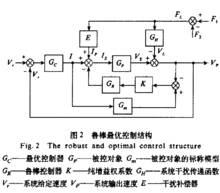

由于并联机器人各通道间存在严重的非线性藕合干扰，使实际系统设计时的鲁棒控制只能削弱或抑制干扰的影响，所以，为提高机器人的操作精度，可同时设计干扰补偿器，对于单一通道，藕合作用集中表现为负载及干扰的影响，即表现为负载压力的变化FL，可选择负载压力FL为观测量，设置补偿器E，通过合理设计即可消除负载及干扰的影响。

在系统中，可通过检测油缸无杆腔的压力F1和有杆腔的压力F2来间接观测负载压力。

由图，Gp，Gm，GR，K实际构成了一个典型的IMC结构。因此，系统对于模型的不确定性和干扰均具有强鲁棒性。采用鲁棒控制器后。被控对象的等效传递函数为

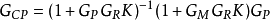
因当K充分大时，Gcp≈Gm，故最优鲁棒控制器Gc可按被控对象标称模型Gm以系统具有最优跟踪特性为目标进行设计，而鲁棒控制器GR可按系统输出干扰影响最小为目标进行设计。两种控制器可分别独立进行设计。4