[科普中国]-自适应同步控制

基本概念自适应控制

自适应控制的研究对象是具有一定程度不确定性的系统，这里所谓的“不确定性”是指描述被控对象及其环境的数学模型不是完全确定的，其中包含一些未知因素和随机因素。

任何一个实际系统都具有不同程度的不确定性，这些不确定性有时表现在系统内部，有时表现在系统的外部。从系统内部来讲，描述被控对象的数学模型的结构和参数，设计者事先并不一定能准确知道。作为外部环境对系统的影响，可以等效地用许多扰动来表示。这些扰动通常是不可预测的。此外，还有一些测量时产生的不确定因素进入系统。面对这些客观存在的各式各样的不确定性，如何设计适当的控制作用，使得某一指定的性能指标达到并保持最优或者近似最优，这就是自适应控制所要研究解决的问题。

自适应控制和常规的反馈控制和最优控制一样，也是一种基于数学模型的控制方法，所不同的只是自适应控制所依据的关于模型和扰动的先验知识比较少，需要在系统的运行过程中去不断提取有关模型的信息，使模型逐步完善。具体地说，可以依据对象的输入输出数据，不断地辨识模型参数，这个过程称为系统的在线辩识。随着生产过程的不断进行，通过在线辩识，模型会变得越来越准确，越来越接近于实际。既然模型在不断的改进，显然，基于这种模型综合出来的控制作用也将随之不断的改进。在这个意义下，控制系统具有一定的适应能力。比如说，当系统在设计阶段，由于对象特性的初始信息比较缺乏，系统在刚开始投入运行时可能性能不理想，但是只要经过一段时间的运行，通过在线辩识和控制以后，控制系统逐渐适应，最终将自身调整到一个满意的工作状态。再比如某些控制对象，其特性可能在运行过程中要发生较大的变化，但通过在线辩识和改变控制器参数，系统也能逐渐适应。

常规的反馈控制系统对于系统内部特性的变化和外部扰动的影响都具有一定的抑制能力，但是由于控制器参数是固定的，所以当系统内部特性变化或者外部扰动的变化幅度很大时，系统的性能常常会大幅度下降，甚至是不稳定。所以对那些对象特性或扰动特性变化范围很大，同时又要求经常保持高性能指标的一类系统，采取自适应控制是合适的。但是同时也应当指出，自适应控制比常规反馈控制要复杂的多，成本也高的多，因此只是在用常规反馈达不到所期望的性能时，才会考虑采用。

同步控制同步控制是和异步控制相对而言的，同步控制的led显示屏在发布和更新内容时，和控制电脑的显示器内容一致，电脑一旦关机则显示屏相应也要关闭。异步控制系统的则不用，一旦发布好内容，连接显示屏的控制电脑关了之后并不影响显示屏的发布。

同步控制是一种常用到的工控技术，同步，顾名思义就是要按照一定比率来协调主机和从机之间的位置、转速、扭矩等量。

多台电机的同步运行问题应用较为广泛，尤其在多单元生产流水线中及驱动同一负载时居多，但对具体的应用，会有不同的要求。若采用变频器及相关配套产品，可较有效地实现不同功能。这里说的配套产品包括：控制电器、变频器辅助选件、传感器、PLC等。

同步控制器一般有两类。一类是和张力系统连同一起来使用的，张力控制器也是一种同步控制器件，这类型的同步是以转速和扭矩等量的同步来实现的；

另一类是空间定位控制器，就是位置同步，一般应用于机器人，数控机床，飞剪等系统的轴间联动使用，是一种轴间的位置跟踪定位。

目前同步控制器有嵌入式设定参数的，也有直接可编程类的，随着技术的发展，可编程类的应用慢慢超过了前者，代表者同步技术的发展方向，它可以通过现场总线等通讯技术和其他设备进行连接和操作。

变频器本身就是一个计算机控制系统，每一种型号的变频器通常适合驱动特定性质的负载。而对于相同负载性质的不同应用需求，希望能够调整变频器参数以满足工艺要求。因此，各种型号的变频器都为用户提供了变频器参数调整的手段。参数调整的方法可以通过配套的操作面板手动离线进行，也可以通过通信的方法在线进行。

研究现状自适应控制为了设计一个满意的控制系统，不论是通常的反馈控制系统，还是最优控制系统，必须事先掌握描述系统运动规律的数学模型及其随环境等变动的情况，否则，用一般的反馈控制方法或最优控制方法是难于设计出满意的控制系统。然而，某些被控对象的数学模型及其环境情况难以明确描述，某些被控对象的特性和环境在系统运行中会发生不可预测的变动，而这是设计者所不能完全掌握的。这些情况的存在，很自然地促使人们产生两种想法:一种是人们根据所有参数都事先设计好，这种方法的代表就是PID调节器;另一种想法就是设计出这样一种调节器或控制器，它不需要人们在现场不断调节，不需要事先详知被控对象的特性，而能在系统运行中自己辨识对象，自行调节控制器本身的结构和参数来满足系统性能的要求，这就是自适应控制思想。利用自适应控制能够解决一些常规的反馈控制所不能解决的复杂控制问题，能大幅度地提供系统的稳定精度和跟踪精度。

在50年代末，由于飞行控制的需要，美国麻省理工学院(MIT)怀特克教授( W hitaker)首先提出飞机自动驾驶仪的模型参考自适应控制方案，称为MIT方案。在该方案中采用局部参数优化理论设计自适应控制规律，这一方案没有得到实际应用。用局部参数优化方法设计模型参考自适应系统，还需检验其稳定性，这就限制了这一方法的应用。在1966年德国学者帕克斯(P.C.Parks)提出采用李雅普诺夫(A.M.Liapunov)第二法来推导自适应算法，以保证自适应系统全局渐近稳定。在用被控对象的输入输出构成自适应规律时，在自适应规律中包含输入和输出的各阶导数，这就降低了自适应对干扰的抑制能力。为了避免这一缺点，印度学者纳朗特兰(K.S.Narendra)和其他学者提出各自的不同方案。罗马尼亚学者波波夫(V.M.Popov)在1963年提出超稳定性理论，法国学者兰道(I.D.Landau) 把超稳定性理论应用到模型参考自适应控制中来。用超稳定性理论设计的模型参考自适应系统是全局渐近稳定的。

自校正调节器是在1973年由瑞典学者阿斯特罗姆(K.J.Astrom) }3z」和威特马克(B . Wittenmark)首先提出来的。1975年克拉开(D.W.Clark)等提出自校正控制器。1979年威尔斯特德(P.E.Wellstead)和阿斯特罗姆提出极点配置自校正调节器和伺服系统的设计方案。最早的直接成果是阿斯特罗姆教授在造纸厂获得成功应用的自校正调节器。从那以后至80年代以前，有关自适应控制的论文虽然很多，但实际成果应用的例子仅有6个：

1)1974年，吉尔巴特和纹斯顿(Gilbart and Winston)利用模型参考自适应控制，使一种光学望远镜的精度提高了5倍以上;
2)1974年，博里森和西丁(Borrison and Syding)在200kW的矿石破碎机中采用自校正控制，使产量提高了约10%;
3)1975年，塞格拉尔和赫德奎斯特(Cegrall and Hedquist)利用类似的自适应方案，改进了造纸机湿度控制回路的性能;
4)1978年，杜蒙和比朗格(Dnmont and Belanger)使工业二氧化钦窑的静态性能改善了10%，动态性能也有改进;
5)1979年，卡尔斯特拉姆等(Kallstrom et al.)在35.5万吨的油轮上采用自校正驾驶控制，使速度提高了;
6)1980年，阿默翁根(Amerongen)在远洋测量船上采用模型参考自适应方法，使平均速度略有提高。

自适应控制经过30多年的发展，无论在理论上或在应用上都取得了很大的进展。进入80年代后，由于计算机的迅速发展，特别是微处理机的广泛普及，为自适应控制的实际应用创造了有利条件。自适应控制在飞行控制、卫星跟踪望远镜的控制、大型油轮的控制、电力拖动、造纸和水泥配料等方面的控制中得到应用。现在，自适应控制在航天、航海、过程控制、电气传动、机器人、经济管理、生物、医学、交通等多方面都取得了可喜的成果。

同步控制复杂网络中同步现象的研究己经有了许多年的历史。最初人们对同步现象的研究主要集中在驱动或祸合的极限环(周期振子)系统的同步(锁相)问题.早期具有开创性的工作始于Winfree。他假设每个振子只与他周围有限个振子之间存在强力作用，这样振子的振幅变化可以忽略，从而将同步问题转化成研究相位变化的问题。后来，Kuramoto指出，一个具有有限个恒等振子的藕合系统，无论系统内部各个振子之间的祸合强度多么微弱，最终他们都可以达到相位同步。此后，祸合系统间的同步问题开始被人们广泛的关注。

随着非线性科学的发展，对同步的概念和基础理论的研究也日趋完善。因而，对复杂系统同步问题的研究也取得了突飞猛进的进展，已经发现了许多不同种类的同步，并且做了相应的研究，如完全同步(complete synchronization) 、广义同步(generalized synchronization)(包括投影同步、部分同步、相位同步、滞后同步、频率同步等)、反同步(anti synchronization)、间歇性滞后同步(intermittent lag synchronization)、弱相同步(imperfect phase synchronization)、几乎完全同步(almost complete synchronization)、外同步(outer synchronization) 等。这些研究成果使得同步这一概念不但能够从物理现象中观察得到，也能够从物理机制上给出严谨的理论证明。同时，在深入的分析复杂网络的拓扑结构之后，发现现实中的大量网络既不是具有不规则网络结构的网络，也不是完全随机网络，而是具有小世界和无标度等共同特性的复杂网络。所以，人们又开始探寻网络的拓扑结构对网络的同步性能造成的影响。针对具有小世界网络模型和无标度网络模型的复杂网络进行了同步分析。在现有的文献中，对于复杂网络同步的研究主要分为两个方面，一个是根据网络本身的拓扑结构，节点的度的分布及聚类系数等特性来研究网络实现同步的能力。另一类则是在给定节点动力学的前提下，考虑在什么样的数学准则下能够实现网络同步。在第一类的问题中，需要通过大量的数值实验和数理统计的方法来比较各类复杂网络的同步能力和揭示网络动力学演化过程中的不同表现行为。这种研究能够用数据来说明复杂网络拓扑结构的祸合矩阵的特征值对系统的同步性能造成的影响。而在进行后一种的研究中。也会涉及到不同拓扑结构的情况。通常在不同的拓扑结构下，得到的能够使网络实现同步的条件也是不相同的。

自适应同步原理Huberman及Lumer于1990年提出用自适应原理控制混沌的方法。John和Amritker在原方法的基础上做了改进，用来控制混沌系统的相空间轨迹与所期望的不稳定轨道达到同步，并用此方法研究了Lorenz及Rossler系统，证明该方法是有效的。

具体地说，自适应同步方法就是利用自适应控制技术来自动调整系统的某些参数，使系统达到混沌同步的目的。 所谓混沌同步，指的是对于从不同初始条件出发的两个混沌系统，随着时间的推移，它们的轨线逐渐一致。应用这一方法有两个前提条件：

①系统至少有一个或多个参数可以得到；

②对于所期望的轨道，这些参数值是己知的。

系统中受控参数的调整还取决于两个因素：

①系统输出变量与所期望轨道的相应变量的差值；

②受控参数值与所期望的轨道相应的参数值之间的差值。

考虑一个n维的自治系统：

X'=f(μ，X)

式中：X是系统状态变量，μ是系统参数集。运用参数自适应原理，将系统的方程化为如下形式：

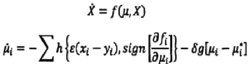
理论上来说，函数h，g可以有很多形式，但是实际上一般取为：

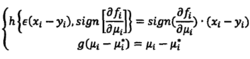研究表明，只要第二个式子的Lyapunov指数均为负数，那么X和Y就可以实现同步。最后，可根据Lyapunov函数原理最终确定式第二个式子中系数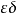的取值范围。1