[科普中国]-级联神经网络

多级神经网络

多年来,人们提出了大量的模式识别方法,这些方法各有优点,但也不可避免地存在一定的局限性和适用条件.为了把各种方法有机地结合起来,取长补短,提高系统的整体性能,人们提出了多级神经网络的结构模型.多级神经网络结构的每一级子系统,通常都由特征提取模块和神经网络模块所组成.特征提取模块从输入数据中提取特征矢量,基于该特征矢量,神经网络模块在学习阶段对所有训练数据进行学习,而在工作阶段则对输入到本级的数据进行分类判别,包括识别输出和拒识输出两种情况.不妨假定:某一级的特征提取模块所提取的特征能有效地代表一部分输入样本的本质特征,因此这一部分样本在该级中将成功地得到识别,其余的样本则由于特征不清而被拒识,送入到下一级进行基于另外一种特征提取和神经网络结构的分类判别。

一个好的多级神经网络结构应满足两个条件:

(1)有效设计每一级的特征提取模块,尽可能使每一级的特征提取方法相互独立,互为补充;

(2)合理设计各级神经网络模块,使得该神经网络能有效地拒识那些在该级特征下模糊不清的样本,从而使误识率尽可能降低.多级神经网络结构的整体性能在很大程度上依赖于每一级子系统误识率的高低,而前几级的误识率尤其关键。1

级联神经网络一般的神经网络是固定好拓扑结构，然后训练权重和阈值。级联相关神经网络是从一个小网络开始，自动训练和添加隐含单元，最终形成一个多层的结构。

级联神经网络(Cascaded Neural Network，以下简称 CNN)，该模型由神经网络组成瀑布结构。所有变量在输入 CNN 之前都要被预处理程序标准化为[0，1]之间，同时，需通过最大相关性最小冗余(Maximum Relevance Minimum Redundancy，以下简称 MRMR)法则的筛选。

结构模型其结构模型如右图所示：

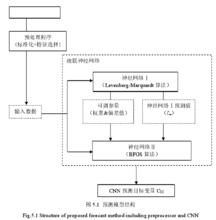
CNN 由神经网络Ⅰ和神经网络Ⅱ组成，两个神经网络分别有不同的学习算法来预测，但具有相同的多层感知器结构（Multi-Layer Perceptron，以下简称 MLP），MLP 有足够数量的隐藏神经元，以至于能够在期望的精度下近似任何连续的多元函数。此外，根据 Kolmogorov 定理，MLP 有适当数量的神经元能够使用一个隐藏层解决问题，因此，本模型中的两个神经网络的 MLP 都具有一个隐藏层。

神经网络Ⅰ会传输两种结果值到神经网络Ⅱ，一种是经过神经网络Ⅰ训练获得地可调参量，包括权重和偏差值，前文提到，两个神经网络具有相同的 MLP，因此，神经网络Ⅰ获得的权重和偏差值可以直接传输给神经网络Ⅱ，从而使神经网络Ⅱ的输出目标变量更加准确；另一种是神经网络Ⅰ预测的目标变量。神经网络Ⅰ向神经网络Ⅱ传输结果值，神经网络Ⅰ的训练会终止，此时，神经网络Ⅱ开始学习进程，以此来取代以往模型中神经网络Ⅱ随机开始。除了神经网络Ⅰ的结果值，一组随机的可调参数初始值也将进入到神经网络Ⅱ的学习进程中，从而保证神经网络Ⅱ获得更加全面的信息。

算法适合的学习算法的选取将使 CNN 比单个神经网络更加全面，将获得更适合的可调参量。Catala 研究得出，Levenberg Marquardt(以下简称 LM)法和 Broyden Fletcher Goldfarb Shanno (以下简称 BFGS)法是基于牛顿法演变出的两个最有效的用于预测的神经网络训练算法。

BFGS算法Broyden Fletcher Goldfarb Shanno 算法 BFGS 算法同样是由优化中的牛顿法演变而来，N. Amjady 认为 BFGS 算法是准牛顿法中最成功的神经网络算法。准牛顿法中，二阶导数的海森矩阵函数将被最小化，不用再对其做其他计算，而是通过分析连续梯度向量来更新海森矩阵。在 BFGS 算法中，以下步骤从初始的猜测值 x0和近似海森矩阵 B0开始重复，直到 x 收敛。

BFGS 算法从一个合适的初始值开始，能够进行更好的解空间收索，神经网络的解空间可以看成一个向量，它的维度是神经网络的可调参量。

LM算法LM 算法是一个快速的学习算法，在训练初期，LM 算法得 MLP能够快速地学习问题，同时，它的训练误差会快速下降。2

级联神经网络交叉验证(Cross-validation)为了避免神经网络产生过拟合，在 CNN中采取交叉验证，交叉验证又被称作循环估计，是一种统计学上将数据样本切割成较小子集的实用方法。运用交叉验证把 CNN 的一部训练集区分出来，当作验证集，而用剩余的训练集来对CNN 中各神经网络进行测试训练，此时，验证集对于各神经网络来说是未知的。各神经网络训练的预测误差对于验证集来说是一个衡量其月度预测误差的标准，神经网络的泛化能力，所谓泛化能力（generalization ability）是指机器学习算法对新鲜样本的适应能力。学习的目的是学到隐含在数据对背后的规律，对具有同一规律的学习集以外的数据，经过训练的网络也能给出合适的输出，也能得到评估。训练和验证的结果越相似，则说明交叉验证的效果越好。各神经网络训练阶段的每一步进程都受验证误差（验证误差为验证集的误差）的限制，当各神经网络在训练时开始出现过拟合，验证误差也会开始上涨，当验证误差上涨到一定限值时，训练将提前终止，从而很准确地防止了过拟合现象的产生。2

性能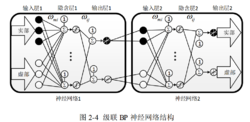通过两个结构不同的神经网络进行级联，可以大大增加网络性能，但这样也会大大加大网络的复杂度，可以从图看出，不管在什么位置增加一个神经元，其资源复杂程度都是倍数增长的，然而在测试中发现，复杂程度的增加在性能的改善上面并不是直接线性关系的，故将网络进行简化，由于神经网络的核心为隐含层和其权值向量，故保留隐含层，将第一层的输出层与第二层的输入层合并，这样可以把双层结构的神经网络复杂度简化为单层的复杂度，通过这样的简化，可以在保证核心隐含层不变的情况下，去掉很大一部分网络结构。3

应用由于级联相关神经网络具有以下优点:学习速度快；自己决定神经元个数和深度；训练集变化之后还能保持原有的结构；不需要后向传播错误信号。级联神经网络可应用于人工成本预测研究、人脸检测方法的研究、年降雨量预测等诸多领域，在电力管理、军事、医疗、智能制造等多个行业也得到了重要应用。