[科普中国]-模糊逻辑过程控制

基本概念

模糊逻辑是建立在多值逻辑基础上，运用模糊集合的方法来研究模糊性思维、语言形式及其规律的科学。模糊逻辑控制(Fuzzy Logic Control)这一概念1974年由L.A.Zadeh教授提出。其核心是对复杂的系统或过程建立一种语言分析的数学模式，使自然语言能直接转化为计算机所能接受的算法语言。

模糊逻辑原理模糊逻辑指模仿人脑的不确定性概念判断、推理思维方式，对于模型未知或不能确定的描述系统，以及强非线性、大滞后的控制对象，应用模糊集合和模糊规则进行推理，表达过渡性界限或定性知识经验，模拟人脑方式，实行模糊综合判断，推理解决常规方法难于对付的规则型模糊信息问题。模糊逻辑善于表达界限不清晰的定性知识与经验，它借助于隶属度函数概念，区分模糊集合，处理模糊关系，模拟人脑实施规则型推理，解决因“排中律”的逻辑破缺产生的种种不确定问题 。

模糊逻辑与计算机结合形成的Fuzzy控制系统为计算机模拟人脑实现复杂控制提供一条途径。Fuzzy控制的基本特征是利用人的经验、知识和推理技术以及控制系统提供的状态条件信息，而不依赖物理过程的精确数学模型，因此简化了复杂的控制问题。

实际上，模糊逻辑是把多值逻辑、概率论、人工智能和神经网络结合在一起，是一门具有坚实的数学理论基础的控方法论，用体现在客观物理系统中的固有印象来仿真人的思维推理。

模糊系统根据语击变量形式的输入做出判断，因为人类是利用语言考虑事物的，变量用少量的IF-THEN(如果/则)规则来测试，根据所采用的规则产生一个或多个响应If描述控制对象的概念，THEN描述由概念作出的操作。每个规则的响应根据其输入的置信度或从属度加权，计算响应曲线以产生适当的输出。模糊逻辑借助人工智能的If-Then结构，但不想人工智能能那样复杂，而又使用少数的规则。神经网络类似模糊逻辑，但它对每一个刺激分配分立的权，而模糊逻辑是一个连续数值状态的系统1。

模糊控制器模糊控制是以模糊集合理论、模糊语言及模糊逻辑为基础的控制，它是模糊数学在控制系统中的应用，是一种非线性智能控制。模糊控制是利用人的知识对控制对象进行控制的一种方法，通常用“if条件，then结果”的形式来表现，所以又通俗地称为语言控制。一般用于无法以严密的数学表示的控制对象模型，即可利用人（熟练专家）的经验和知识来很好地控制。因此利用人的智力模糊地进行系统控制的方法就是模糊控制2。

如图1所示，模糊控制器的基本结构包括知识库、模糊推理、输入量模糊化、输出量精确化四部分。

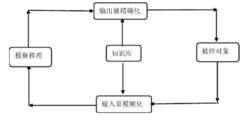图1

（1）知识库

知识库包括模糊控制器参数库和模糊控制规则库。模糊控制规则建立在语言变量的基础上。语言变量取值为“大”、“中”、“小”等这样的模糊子集，各模糊子集以隶属函数表明基本论域上的精确值属于该模糊子集的程度。因此，为建立模糊控制规则，需要将基本论域上的精确值依据隶属函数归并到各模糊子集中，从而用语言变量值(大、中、小等)代替精确值。这个过程代表了人在控制过程中对观察到的变量和控制量的模糊划分。由于各变量取值范围各异，故首先将各基本论域分别以不同的对应关系，映射到一个标准化论域上。通常，对应关系取为量化因子。为便于处理，将标准论域等分离散化，然后对论域进行模糊划分，定义模糊子集，如NB、PZ、PS等。

同一个模糊控制规则库，对基本论域的模糊划分不同，控制效果也不同。具体来说，对应关系、标准论域、模糊子集数以及各模糊子集的隶属函数都对控制效果有很大影响。这3类参数与模糊控制规则具有同样的重要性，因此把它们归并为模糊控制器的参数库，与模糊控制规则库共同组成知识库。

（2）模糊化

将精确的输入量转化为模糊量F有两种方法:

a.将精确量转换为标准论域上的模糊单点集。

精确量x经对应关系G转换为标准论域x上的基本元素.

b.将精确量转换为标准论域上的模糊子集。

精确量经对应关系转换为标准论域上的基本元素，在该元素上具有最大隶属度的模糊子集，即为该精确量对应的模糊子集。

（3）模糊推理

最基本的模糊推理形式为:

前提1 IF A THEN B

前提2 IF A′

结论 THEN B′

其中，A、A′为论域U上的模糊子集，B、B′为论域V上的模糊子集。前提1称为模糊蕴涵关系，记为A→B。在实际应用中，一般先针对各条规则进行推理，然后将各个推理结果总合而得到最终推理结果。

（4）精确化

推理得到的模糊子集要转换为精确值，以得到最终控制量输出y。目前常用两种精确化方法：

a.最大隶属度法。在推理得到的模糊子集中，选取隶属度最大的标准论域元素的平均值作为精确化结果。

b.重心法。将推理得到的模糊子集的隶属函数与横坐标所围面积的重心所对应的标准论域元素作为精确化结果。在得到推理结果精确值之后，还应按对应关系，得到最终控制量输出y。

意义模糊控制拥有很多的优势，比如简化系统设计的复杂性，特别适用于非线性、时变、模型不完全的系统上。模糊控制技术利用控制法则来描述系统变量间的关系。同时不用数值而用语言式的模糊变量来描述系统，模糊控制器不必对被控制对象建立完整的数学模式。模糊控制器是一语言控制器，使得操作人员易于使用自然语言进行人机对话。模糊控制器是一种容易控制、掌握的较理想的非线性控制器，并且抗干扰能力强，响应速度快，并对系统参数的变化有较强的鲁棒性和较佳的容错性。最后它是从属于智能控制的范畴。该系统尤其适于非线性，时变，滞后系统的控制3。

（1）运用模糊逻辑变量、模糊逻辑函数和似然推理等新思想、新理论，为寻找解决模糊性问题的突破口奠定了理论基础，从逻辑思想上为研究模糊性对象指明了方向。

（2）模糊逻辑在原有的布尔代数、二值逻辑等数学和逻辑工具难以描述和处理的自动控制过程、疑难病症的诊断、大系统的研究等方面，都具有独到之处。

（3）在方法论上，为人类从精确性到模糊性、从确定性到不确定性的研究提供了正确的研究方法。

此外，在数学基础研究方面，模糊逻辑有助于解决某些悖论。对辩证逻辑的研究也会产生深远的影响。当然，模糊逻辑理论本身还有待进一步系统化、完整化、规范化。