[科普中国]-自适应神经模糊系统

基本概念

模糊逻辑和神经网络近年来发展较快，模糊推理系统非常适于表示模糊的经验和知识，但缺乏有效的学习机制；神经网络虽然具有自学习功能，却又不能很好的表达人脑的推理功能。基于自适应神经网络的模糊推理系统ANFIS(Adaptive Network-based Fuzzy Inference System)将二者有机的结合起来，既发挥了二者的优点，又弥补了各自的不足。自适应神经网络模糊系统其中一个十分重要的应用，就是在信号处理和控制中消除噪声或干扰1。

J-S.R.Jang提出的自适应神经模糊推理系统是一种将模糊逻辑和神经元网络有机结合的新型的模糊推理系统结构，采用反向传播算法和最小二乘法的混合算法调整前提参数和结论参数，并能自动产生If-Then规则。

ANFIS的结构ANFIS是一种基于Takagi-Sugeno模型的模糊推理系统，它将模糊控制的模糊化、模糊推理和反模糊化3个基本过程全部用神经网络来实现，利用神经网络的学习机制自动地从输入输出样本数据中抽取规则，构成自适应神经模糊控制器，通过离线训练和在线学习算法进行模糊推理控制规则的自调整，使其系统本身朝着自适应、自组织、自学习的方向发展。

为简单起见，假定所考虑的模糊推理系统有2个输入x和y，单个输出z。对于一阶Takagi-Sugeno模糊模型，如果具有以下2条模糊规则：

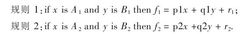
一阶T-S模糊推理系统的ANFIS网络结构如图12。

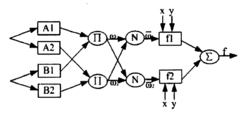图1

ANFIS控制器由于采用了Sugeno型模糊规则和加权求和法计算总输出，省去了常规模糊系统用重心法进行清晰化的大量计算工作，使得数据处理最大限度地简化。

各个节点的重要功能如下：

第1层：将输入变量模糊化，输出对应模糊集的隶属度所以可以称为模糊化层。该层的每个结点i是一个有结点函数的自适应结点。

第2层：实现前提部分的模糊集的运算。在这一层中的每个结点都是固定结点，它的输出是所有输入信号的代数积。每个结点的输出表示一条规则的激励强度，本层的结点函数还可以采用取小、有界积或强积的形式。

第3层：将各条规则的激励强度归一化，该层中的结点也是固定结点。

第4层：这一层的每个结点i是一个有结点函数的自适应结点，计算出每条规则的输出。

第5层(输出层)：这一层的单结点是一个标以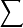的固定结点，它计算所有传来信号之和作为总输出。

ANFIS的学习算法神经模糊控制器的主要作用是应用神经网络自学习能力，寻求和调整神经模糊控制系统的参数和结构。模糊控制器需要两种类型的调整：结构调整和参数调整。结构调整包括变量数目、输入输出变量论域的划分、规则的数目等。一旦获得了满意的结构后，就需要对参数进行调整。参数调整包括与隶属函数有关的参数，如中心、宽度、斜率等。ANFIS的学习算法实际上只是对控制器的参数进行学习，因为网络结构已经确定，只需调整前提参数和结论参数即可。

有四种法用来更新参数，按照复杂的程度表述如下：

(1) Gradient Descent Only：所有参数都用梯度下降法进行更新。

(2) radient Descent and Once Pass of LSE(Least Squares Estimate)：最小二乘法仅用一次，即只在最开始时用以得到初始的结论参数，然后就只用梯度下降法来更新所有的参数。

(3) Gradient Descent and LSE：梯度下降法和最小二乘法。

(4) Sequential (Apporoximate) LSE Only：即仅用递推(近似)最小二乘法。

选择那种方法，应综合考虑计算的复杂度和所要达到的性能3。

应用及发展非线性系统建模问题是目前学术界研究的热点问题。常用的传统非线性系统描述方法有微分（或差分）法、泛函级数法、NARMAX模型法及分块系统法等。但是对于一个非线性、多变量的复杂系统，用常规的数学方法建模既费时又费力，而且在各种假设下建模，其适应性也不好。而J-S.R.Jang提出的自适应神经模糊推理系统是一种将模糊逻辑和神经元网络有机结合的新型的模糊推理系统结构，采用反向传播算法和最小二乘法的混合算法调整前提参数和结论参数，并能自动产生If-Then规则。

自适应神经网络模糊系统是一种采用Takagi-Sugeon模型的模糊推理系统。它为模糊建模的过程提供一种能够从数据集中提取相应信息（模糊规则）的学习方法，通过学习能有效的计算出隶属度函数的最佳参数，使得设计出来的Sugeon型模糊推理系统能最佳的模拟出所希望的输入输出关系，所以ANFIS是一种基于已有数据的建模方法。ANFIS具有以下特点：

(1)随着模糊逻辑和神经网络的发展，这两种理论结合的产物一自适应神经网络模糊推理系统由于同时具有模糊逻辑易于表达和神经网络自学习能力的优点，成为近年来计算智能学科的一个重要研究方向。

(2) Sugeon型模糊推理具有计算简单、利于数学分析的特点，且易于和自适应方法结合，从而为复杂系统的建模和控制提供了有效的工具。尤其是在信号处理中消除噪声干扰、提高测量精度等方面具有十分重要的应用。