[科普中国]-不确定离散系统

基本概念不确定系统

系统的诸因素中含有不能用确定的量进行描述的系统或呈现有不确定性信息的系统称为不确定性系统。所谓不确定，即不明确、不肯定。不确定的量是表述系统中不确定性信息的量，如模糊量、灰色量，都是不确定的量，分别称之为模糊不确定量、灰色不确定量。

不确定性系统预测的基本出发点是强调以系统思想为指导，以综合处理不确定性信息为主要手段。它没有改变经典预测的初衷，是经典预测的继承和发展。因此，经典预测理论的基本原理在此仍具有指导作用。

离散系统早在五十年代，由于数字计算机在工程和科学上应用的增加，离散控制系统的研究己经引起了人们的注意，当时的工作主要是应用z变换研究采样数据系统。近三十年来，离散控制系统的研究已经有了较大的发展。尤其是近几十年来，随着科学技术的高速发展，人类社会进入到信息化，工业技术发生了根本性变革，出现了一大批高新技术领域世界范围的微电子技术革命浪潮，极大地推动了微处理机和微型计算机在控制系统种的应用。由于数字计算机进行计算机时在时间上是离散的，因此当一个系统用数字计算机进行控制或用数字计算机模拟、分析、设计控制系统时，需要把时间变量考虑为离散变量，研究的系统需要考虑为离散系统，由于这些原因，近来离散控制系统的研究再次引起了控制界的特别重视，目前离散控制系统的分析与设计已成为控制理论的一个重要组成部分。

随着微型机的多功能性及可靠性的不断提高，加之其价格的日益下降，应用微型计算机进行控制和管理日益广泛。例如用小型机代替二次仪表对生产过程进行控制时，其不仅可以实现PID控制，还可以实现一些复杂控制。更进一步，还可以应用离散控制系统的理论和方法，设计更高级的反馈系统，以达到诸如最优控制、线性多变量控制、自适应控制等等。又如用微机对一个工厂、一个公司以至一个比较复杂的管理系统管理时，通过建立数学模型，利用离散系统的理论和方法进行分析与设计，可以得到令人满意的管理策略。由于数字计算机处理的只能时离散的数字信号，所以，不论它用于控制或用于管理，如果原来的信号时连续的，都需要将它离散化，转换成离散信号。这就是说，需要通过离散化把原来的连续控制系统转换成一个离散控制系统来处理。因此研究离散系统具有重要的现实意义。

研究背景在实际的工业控制中，各种工业生产过程，生产设备以及其他众多被控对象，其动态特性一般都难以精确的数学模型描述。有时即使能获得被控对象数学模型，但由于其过于复杂，也难以对其进行有效的性能分析和综合，因此必须进行适当的简化。另一方面，随着生产过程中条件和环境的变化，控制系统中元件的老化或损坏，被控对象本身的特性也会随之发生变化，所有这些因素使得描述被控对象的数学模型和实际对象之间不可避免的存在一定的误差。因此，不确定性普遍存在于工程应用中。例如汽车离合器变速缓冲装置，应用H∞控制理论来改善自动离合器变速时的过渡响应，从而提高舒适性的实例。另一个常见的例子是矿车速度控制，矿车在运行过程中，车速的变化或坑道坡度的变化会引入钢索的伸缩振动，且在坑道各站停车时，矿车会来回振动，从而不仅恶化乘客的舒适感而且降低工作效率。不确定系统有个显著的特点就是系统中存在未知的不确定项。不确定系统的控制系统的设计与实现，要求存在未知不确定性的情况下，仍然能使系统稳定并保持所希望的系统性能。

模型的分类方法就不确定离散系统而言，其不确定性产生的原因很多，主要包括：

(1)参数的测量误差；

(2)参数的辨识误差；

(3 )参数的实际值与标称值的偏差；

(4)环境和运行条件的影响，这往往是不确定性的最重要的原因；

(5)工况变动的影响；
(6)人为的简化等等。

将不确定系统模型扩展到反馈控制系统设计中，控制器模型C(s)和控制对象模型P(s)以及系统的不确定性△(s)的关系如图所示：

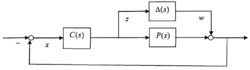
其中不确定△(s)包括了系统的不确定摄动等因素。从不确定性的分类来看，一般将其分为三类：

1.可参数化不确定性模型。可参数化不确定模型又称参数不确定性，是指可以用被控对象模型的参数摄动来表示不确定性.这类不确定性一般不改变系统的结构。例如矩形体、球形体、多面体内取值等。
2.非结构性摄动。这种摄动不仅以参数变化形式出现而且系统结构也发生变化，例如H∞范数，Gap度量的摄动。
3.混合摄动。同时具有结构性和非结构性摄动。

纵观不确定系统的研究和发展，存在两条主要的线索，即基于传递函数矩阵的频域理论与直接状态空间模型的时域理论。非结构不确定在频域分析中应用较多。1

不确定离散系统的鲁棒控制在鲁棒控制理论的发展中形成了一些理论分支，如H∞控制理论、结构奇异值理论和Kharitonov区间理论等，在这些鲁棒控制理论中我们主要介绍一下H∞控制理论。在二十世纪60年代，以状态空间描述对象的现代控制理论得到了很大发展，出现了以Kalman-Bucy滤波器和最优二次调节理论为基础的LQG设计方法，这种设计方法忽略了系统的不确定性，对系统的干扰作了很严格的要求，它要求精确的系统模型，如果系统的模型具有不确定性，LQG设计方法就不能保证系统具有鲁棒性。Zames 指出：基于状态空间模型的LQG设计方法之所以鲁棒性不好，主要是LQG使用的积分指标造成的以及将不确定的干扰用白噪声模型表示。基于此，他提出，假定干扰属于某一己知信号集的情况下，用其相应的灵敏度函数的H∞范数作为指标，设计目标是在可能发生的最严重干扰下使系统的误差在这种范数意义下达到极小，这样就将干扰问题转化位求解使闭环系统稳定，并使相应的H∞范数指标极小化的输出反馈控制问题。H∞控制的基本思想是用H∞范数作为目标函数的度量进行控制系统的设计，使系统干扰至误差的传递函数的H∞范数最小，从而使具有有限功率谱的干扰至误差影响降到最小程度。H∞控制本质上可以认为是鲁棒控制的一个分支，最初的H∞控制问题不是考虑系统的参数不确定性，而是考虑系统干扰的不确定性，后来发展的鲁棒H∞控制理论，同时考虑系统参数不确定性和干扰对系统性能的影响。

一般认为Zames (1981)提出的以控制系统内的某些信号间的传递函数矩阵H∞范数为优化指标的设计思想标志着H∞控制理论的诞生。其后一段时期的问题主要是在控制系统内部稳定的控制器集合中寻求一个传递函数矩阵的H二范数的最小解问题。Doyle等人(1989)在美国控制年会上发表了著名DGKF论文，证明了可通过求解两个适当的代数Riccati矩阵方程来得到H∞控制的解。DGKF的论文标志着H∞控制理论的成熟。在H∞控制的研究中，有界实引理的引进以及其和H∞控制之间关系的建立为H∞控制的研究提供了新的工具，使得可以更加简洁有效地证明DGKF论文的主要结论。有界实引理也为应用不确定系统二次镇定的Riccati方程方法来研究不确定系统的鲁棒H∞控制问题提供了可能。

不确定离散系统的保成本控制不确定性系统的保成本控制(GCC)最早是由Chang和Peng于1972年在自适应控制中提出来的。近年来，随着不确定系统鲁棒二次镇定和H∞控制状态空间方法研究所取得的进展，保成本控制问题研究再次受到人们的注意，吸引了众多专家学者，并取得了令人注目的成果。其研究己经贯穿控制系统的各个领域，如线性连续不确定系统、离散不确定系统、时滞系统、不确定系统以及不确定广义系统等。

在工业过程系统中，各个元件(主要是执行器和传感器)往往会随着控制系统运行时间的不断增加出现损坏或发生失效，从而导致整个系统不稳定或性能变差。为了让控制系统在某些元件出现失效时仍具有一定程度的可靠性，系统能够正常运行并达到设定的性能指标，有些学者提出了可靠控制理论。最初的可靠控制理论的研究大多是针对确定系统的并结合等的性能指标要求，设计合适的反馈控制律。

Veillette完整的介绍了集中式和分散式两种类型的可靠控制设计方案，研究了具有参数不确定的单扰动系统的可靠保成本问题，通过将满阶的代数Riccati方程分解为两个降阶的快速代数Riccati方程来避免由并行计算引起的僵直问题。Yu 首先研究了在给定的二次成本函数下的离散时间系统的可靠保成本控制，并且所用的执行器的失效模型是一个新的模型，包括了所有失效的情况，具有更广泛的意义。线性矩阵不等式处理方法的应用也更方便的给出了最优可靠保成本控制律的参数表达形式。2