[科普中国]-模糊自适应预测控制

基本概念

针对带有时滞、不确定性的工业过程， 模糊自适应预测控制不需要过程的数学模型，只要在线检测过程的实际输出和期望输出，通过模糊预测控制校正无辨识自适应控制律，即可以对时滞、建模困难的工业过程实现自适应控制。

带有不确定性工业过程的控制问题一直是困扰控制理论和控制工程实践的难题，而带有时滞、不确定性工业过程的控制更加困难。但是不确定、滞后现象是实现工业过程中普遍存在的一种现象，因此对于这类对象控制问题的研究具有重要理论和现实意义。目前对于带有不确定性对象的控制主要采用自适应控制、鲁棒控制等方法，而过程的时滞特性通常用预测控制等方法加以克服，但是这些先进技术都是建立在过程模型确定的基础上1。

结构由Marsik和Strejc提出的无辨识自适应控制算法不需要辨识过程参数，只需在线检测过程实际输出及期望输出，这种自适应算法简单，并且在工业过程控制中己得到成功的应用。

模糊自适应预测控制器中模糊预测的功能是在每个采样时刻，根据过程实际输出逼近期望输出来估计控制系统的性能并修正无辨识自适应控制律。

模糊自适应预测控制器结构图如下2：

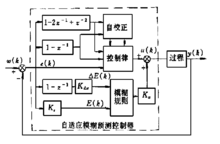图1

模糊自适应控制方法自适应预测控制方法(1)预测模型

预测控制应具有预测功能，即能够根据系统的现时刻的控制输入以及过程的历史信息，预测过程输出的未来值，因此，需要一个描述系统动态行为的模型作为预测模型。

在预测控制中的各种不同算法，采用不同类型的预测模型，如最基本的模型算法控制(MAC)采用的是系统的单位脉冲响应曲线，而动态矩阵控制(DMC)采用的是系统的阶跃响应曲线。这两者模型互相之间可以转换，且都属于非参数模型，在实际的工业过程中比较容易通过实验测得，不必进行复杂的数据处理，尽管精度不是很高，但数据冗余量大，使其抗干扰能力较强。

预测模型具有展示过程未来动态行为的功能，这样就可像在系统仿真时那样，任意的给出未来控制策略，观察过程不同控制策略下的输出变化，从而为比较这些控制策略的优劣提供了基础。

(2)反馈校正

在预测控制中，采用预测模型进行过程输出值的预估只是一种理想的方式，在实际过程中。由于存在非线性、模型失配和干扰等不确定因素，使基于模型的预测不可能准确地与实际相符。因此，在预测控制中，通过输出的测量值Y(k)与模型的预估值Ym(k)进行比较，得出模型的预测误差，再利用模型预测误差来对模型的预测值进行修正。

由于对模型施加了反馈校正的过程，使预测控制具有很强的抗扰动和克服系统不确定性的能力。预测控制中不仅基于模型，而且利用了反馈信息，因此预测控制是一种闭环优化控制算法。

(3)滚动优化

预测控制是一种优化控制算法，需要通过某一性能指标的最优化来确定未来的控制作用。这一性能指标还涉及到过程未来的行为，它是根据预测模型由未来的控制策略决定的。

但预测控制中的优化与通常的离散最优控制算法不同，它不是采用一个不变的全局最优目标，而是采用滚动式的有限时域优化策略。即优化过程不是一次离线完成的，而是反复在线进行的。在每一采样时刻，优化性能指标只涉及从该时刻起到未来有限的时间，而到下一个采样时刻，这一优化时段会同时向前。所以，预测控制不是用一个对全局相同的优化性能指标，而是在每一个时刻有一个相对于该时刻的局部优化性能指标。

(4)参考轨迹

在预测控制中。考虑到过程的动态特性，为了使过程避免出现输入和输出的急剧变化，往往要求过程输出y(k)沿着一条期望的、平缓的曲线达到设定值r。这条曲线通常称为参考轨迹y，。它是设定值经过在线“柔化”后的产物。

模糊自适应控制算法对于随机过程的动态系统，无法测辨其系统模型而采用模糊控制机制解决这一问题。如图为模糊自适应控制器结构：

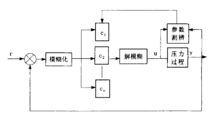图2

模糊控制器的基本结构包括知识库、模糊推理、输入量模糊化、输出量精确化四部分。

（1）知识库

知识库包括模糊控制器参数库和模糊控制规则库。模糊控制规则建立在语言变量的基础上。语言变量取值为“大”、“中”、“小”等这样的模糊子集，各模糊子集以隶属函数表明基本论域上的精确值属于该模糊子集的程度。因此，为建立模糊控制规则，需要将基本论域上的精确值依据隶属函数归并到各模糊子集中，从而用语言变量值(大、中、小等)代替精确值。这个过程代表了人在控制过程中对观察到的变量和控制量的模糊划分。由于各变量取值范围各异，故首先将各基本论域分别以不同的对应关系，映射到一个标准化论域上。通常，对应关系取为量化因子。为便于处理，将标准论域等分离散化，然后对论域进行模糊划分，定义模糊子集，如NB、PZ、PS等。

同一个模糊控制规则库，对基本论域的模糊划分不同，控制效果也不同。具体来说，对应关系、标准论域、模糊子集数以及各模糊子集的隶属函数都对控制效果有很大影响。这3类参数与模糊控制规则具有同样的重要性，因此把它们归并为模糊控制器的参数库，与模糊控制规则库共同组成知识库。

（2）模糊化

将精确的输入量转化为模糊量F有两种方法:

a.将精确量转换为标准论域上的模糊单点集。

精确量x经对应关系G转换为标准论域x上的基本元素.

b.将精确量转换为标准论域上的模糊子集。

精确量经对应关系转换为标准论域上的基本元素，在该元素上具有最大隶属度的模糊子集，即为该精确量对应的模糊子集。

（3）模糊推理

最基本的模糊推理形式为:

前提1 IF A THEN B

前提2 IF A′

结论 THEN B′

其中，A、A′为论域U上的模糊子集，B、B′为论域V上的模糊子集。前提1称为模糊蕴涵关系，记为A→B。在实际应用中，一般先针对各条规则进行推理，然后将各个推理结果总合而得到最终推理结果。

（4）精确化

推理得到的模糊子集要转换为精确值，以得到最终控制量输出y。目前常用两种精确化方法：

a.最大隶属度法。在推理得到的模糊子集中，选取隶属度最大的标准论域元素的平均值作为精确化结果。

b.重心法。将推理得到的模糊子集的隶属函数与横坐标所围面积的重心所对应的标准论域元素作为精确化结果。在得到推理结果精确值之后，还应按对应关系，得到最终控制量输出y。

优势基于模糊预测的无辨识自适应控制是一种适合于复杂工业过程控制的有效方法，具有广阔的应用前景。其优点在于：

（1）控制算法非常简单，适合于大滞后复杂过程的实时控制。

（2）对控制过程的数学模型没有任何要求，适合于解决工业过程中难以建立数学模型的复杂对象的控制问题。

对于非线性、不确定的动态系统，采用自适应类控制，可以实时跟踪受控过程的结构参数和模型参数，以达到自校正控制目吮但这类控制，对过程的数学模型的精度要求较高，大多数的实际控制都难以做到。针对受控过程表现出的“黑箱”特性和“灰箱”特性，采用模糊控制方案，可以克服自适应类控制的缺陷。控制算法是基于自适应采样控制，这也同时保持了参数跟踪特性，使得控制性能得到优化所给的算法简洁实用，且易于实现，适合于大多数工业过程控制采用3。