[科普中国]-升力分布

升力

升力，就是向上的力。 使你上升的力。 有很多种了。一般都是说在空气中。 也就是向上的力大于向下的力，其合力可以使物体上升。 这个力就是升力。升力的成因较复杂，因为要考虑实际流体的粘性、可压缩性等诸多条件。目前大多用的是库塔儒可夫斯基定理，它是工程师计算飞机升力最精确的方法。具体内容就是由绕翼环流导致升力，产生了上下压力差，这个压力差就是升力 (Y)，升力和向后的诱导阻力（d）合成为空气动力（R）。流过各个剖面升力总合就是机翼的升力。升力维持飞机在空中飞行。

升力来源于机翼上下表面气流的速度差导致的气压差。但机翼上下表面速度差的成因解释较为复杂，通常科普用的等时间论和流体连续性理论均不能完整解释速度差的成因。航空界常用二维机翼理论，主要依靠库塔条件、绕翼环量、库塔-茹可夫斯基定理和伯努利定理来解释。

准静弹性飞机升力分布刘千刚等介绍了一种准静弹性飞机气动特性的数值计算方法。可以用它来计算亚音速时弹性飞机的升力分布及11个主要的纵向气动导数。

数值计算方法是目前研究弹性飞机气动特性重要手段之一。由于这一计算牵涉到气动、结构、飞行力学等几个方面的问题，工作量较大，需要选择合适的方法。

他们在气动力计算方面，采用了格林定理所导出的速势积分方程方法。其主要优点是能适用于各种复杂外形飞行器的气动力计算，且所费机时较少，结果比较准确，因而比较适合于弹性飞行器的气动力计算。在结构变形计算方面，采用了自由结构影响系数方法。这一方法不仅正确地解决了自由飞行中飞机结构变形的计算间题，而且由于所得出的弹性飞机气动导数及其所适用的运动方程在形式上与刚性飞机的完全相同，也给分析和研究弹性飞机的动态特性带来很多方便。

弹性飞机在一定的高度一定的M数作水平等速直线飞行时，下述方程组成立：

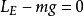
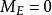
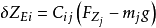
式中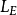 为弹性飞机的升力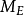， 为弹性飞机的俯仰力矩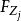， 为作用在弹性飞机小块元素上的升力。 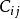称为自由结构影响系数，它表示自由飞行中的飞机在j元素上受到一单位外力的作用，在i元素处所产生的弹性位移。 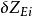表示飞机各元素的弹性位移。

由方程组，可以确定弹性飞机在一定的M数、一定的高度作水平等速直线飞行时的攻角、舵偏角以及此时飞机的升力分布及升力系数、诱导阻力系数。1

相关软件陈后立等采用Advanced AircraftAnalysis2.4(AAA2.4)软件对一架超小型固定翼飞行器(SMAV)机翼、平尾、垂尾升力系数分别做了计算,并给出相应的顺翼展方向升力分布、顺平尾展方向升力分布、顺垂尾展方向升力分布。最后给出了该架超小型固定翼飞行器的升力与攻角变化曲线图。

Advanced AircraftAnalysis 2.4(AAA2.4)是由Dar-corporation公司开发的专门用于飞行器设计、分析和研究的大型软件。利用该软件我们可以对SMAV进行重量、尺寸、开环和闭环动态稳定性和灵敏性等分析。由于SMAV涉及的空气动力系数很多且相当复杂，陈后立等主要应用其中的空气动力学模块中的升力计算模块对SMAV的升力系数进行计算。2

目标环量分布近年来，无人机由于其特有的技术优势和突出性能，成为了未来航空飞行器的重要发展方向。无人机的飞行主要划分为起飞阶段、空中巡航阶段和着陆阶段，其中巡航是无人机飞行的主要阶段。在巡航阶段，机翼阻力的大小直接决定其耗油量和续航时间。根据Breguet关系式可知，机巽升阻比的增加或阻力的减小均可增大航程，若保持航程不变，则可减轻燃料重量。无人机巡航飞行时，诱导阻力占总阻力的40%，因此为了优化升阻比，研究如何减小诱导阻力是十分必要的。

减小诱导阻力的措施主要有：在翼梢处加装翼梢小翼，这种方法能够有效抑制机翼下表面气流上卷形成的翼尖旋涡，从而达到增升减阻的目的，提高飞机的巡航时间。目前这种技术相对成熟，己广泛应用在大型民用飞机中。另一种减小诱导阻力的方法是改变机翼的展向升力分布形式。

空气动力学研究表明，机翼的诱导阻力与沿翼展方向的升力分布形式密切相关，在展向升力分布为椭圆形时诱导阻力最小。在飞机气动外形初步设计阶段，升力分布形式取决于机翼的梢根比，通过选择合适的梢根比可得到理想的环量分布。为了进一步提高机翼的气动性能，许多学者提出了优化的设计方法。

为了优化直升机升阻比，研究了飞机设计过程中减小诱导阻力的措施，提出了一种机翼几何扭转角的反向设计方法。该方法通过确定目标升力分布形式，对沿翼展方向选取的设计点进行几何扭转角设计，实现目标分布。基于升力线理论，建立用傅里叶正弦级数表示的升力线理论积分微分方程的矩阵表示形式，编制了低速平直机翼的气动力、气动载荷分布的计算程序和几何扭转角的反向设计程序。最后，基于目标环量分布获得了几何扭转机翼，并通过程序预测和数值模拟方法对优化结果进行了仿真。计算结果表明：设计后的几何扭转机翼展向环量分布达到目标椭圆分布形式，几何扭转机翼诱导阻力减小了17.07%，总阻力减小了15.43%，计算状态升阻比提高了6.5%。该方法对选取控制剖面进行设计，可实现性较强，具有一定工程应用价值。3