[科普中国]-诱导转捩

简介

线性稳定性理论无法解释钝体头部边界层的失稳机制。因为，根据这个理论，钝体头部流场，对所有单频波的扰动都是稳定的。因而，利用这种方法对钝体进行的转捩预测，其转捩位置都在远离头部的锥身上。但widhopf和Hall的地面实验表明，在某些条件下，转捩位置是在钝锥的头部，并不是在锥身。这一点也可以从美国的NRV、回收的Gemini返回舱以及我国神州一号返回舱的烧蚀外形上得到了证实。

近年来，人们已经认识到并开始研究的诱导转捩现象。它不同于通常所说的小扰动转捩或自然转捩。自然转缺是当流动超过临界雷诺数后，由理论上无限小振幅的扰动引起的，大体上由以下3个主要阶段组成：(1)首先由层流边界层内有选择性的小扰动，形成二维不稳定的T-S波；(2)随着扰动增长，导致三维非定常扰动波的形成；(3)三维扰动波的继续发展，使得在当地高涡量处产生湍流斑。湍流斑的持续出现和扩散，最终形成湍流边界层。诱导转捩实际上有限幅值扰动引发的直接非线性转捩，又称为大扰动转捩。这种类型的转捩，本质上是由某种形式的非线性扰动引起的。当这种扰动强度大到能够直接激励出非线性相互作用时，扰动的演化过程将跳过自然转捩的前两个阶段，直接形成湍流斑，从而迅速进人湍流。在此过程中，扰动的非线性增长是湍流斑形成的主要原因。它既可发生在流场中的线性不稳定区域，也可发生在线性稳定的区域中。1

局部大扰动诱导转捩的物理机理研究研究介绍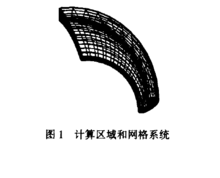该研究利用高精度、高分辨率紧致格式，以及激波装配和在出口边界处高分辨率的无反射边界处理技术，对钝锥端头超声速部分的曲壁边界层内的局部有限幅值扰动的演化过程，进行了直接数值模拟。模拟结果，清楚地揭示了诱导转捩的发生、发展过程和非线性相互作用的物理机制。1

结果与讨论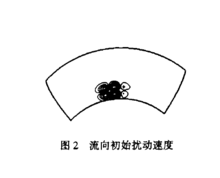初始流场的状态参数为：Ma=6.0，Re=1000000，T∞=100K，TW=300K。计算外形是6°钝锥。为提高效率，在计算时，先采用轴对称N-S方程和激波装配技术。计算网格点为241×241。在得到轴对称流场的结果后，利用绝热流动总熔相等的概念确定钝头体的边界层的名义厚度δ，取1.5占作为法向高度；流向取声速线以后部分，约40°到球、锥结合处；周向取90°周角范围作为直接数值模拟的计算区域。网格系统见图1。初始扰动的形态如图2所示，图2是法向坐标面上的流向扰动速度。

该研究利用数值方法，采用更接近真实物理过程的空间模式，模拟了引人球锥端头超声速边界层流动中的类似湍涡结构的非线性扰动的演化过程，研究了反转旋涡导致流动失稳的物理机制，得到了下面的结论：

(1)初始扰动的涡结构的形态对是否能最终导致流场失稳有很大关系。涡结构的法向尺度太小或涡系的中心位置过于靠近壁面，在一定时空的范围内，不会造成流动失稳。

(2)脱涡频率也是能否导致流场最终失稳的关键参数之一。只有当脱涡频率达到一定程度时，才有湍流斑出现。

(3)在一定条件下，三维流动中引人的涡结构将发生对并和拉伸，扰动幅值迅速增长。并将最终导致层流流动的崩溃。

(4)湍流斑与流场中涡的对并、拉伸以及诱导出新的涡结构有关，但并非是由于“发卡”的两臂崩溃造成的，而是由于“发卡”的头部变形和不断诱导出新的涡结构,以及涡结构之间的相互作用造成的。

(5)诱导转捩是由于扰动直接激励起的类似湍涡这样的非线性结构的运动、发展造成的，没有出现线性失稳的过程。1