[科普中国]-不确定混沌系统

基本概念不确定系统

系统的诸因素中含有不能用确定的量进行描述的系统或呈现有不确定性信息的系统称为不确定性系统。所谓不确定，即不明确、不肯定。不确定的量是表述系统中不确定性信息的量，如模糊量、灰色量，都是不确定的量，分别称之为模糊不确定量、灰色不确定量。

不确定性系统预测的基本出发点是强调以系统思想为指导，以综合处理不确定性信息为主要手段。它没有改变经典预测的初衷，是经典预测的继承和发展。因此，经典预测理论的基本原理在此仍具有指导作用。

混沌混沌，一般是指确定性系统中出现的一种貌似无规则的，类似随机的现象。这里，“确定性系统”是指混沌系统由确定的动力系统描述，其响应也是确定的。但人们发现一些系统中，特别是非线性系统中体现出了类似随机的复杂状态，表现为系统长期行为的不可预测性，即一个系统的演变过程对初态非常敏感，在科学上，人们就把具有上述现象的系统称为混沌系统。总而言之，混沌的本质是系统的长期行为对初始条件的敏感性，如我们常说“差之毫厘，失之千里”、蝴蝶效应等等。混沌是非线性系统普遍具有的一种复杂动力学行为，被称为是20世纪最重要的科学发现之一。

不确定混沌系统的动力学模型考虑一类状态和输出均受扰的参数不确定混沌系统：

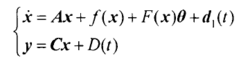
其中，x是系统的状态向量；y是系统的标量输出；f(x)和F(x)是非线性函数；A，C是已知的系数矩阵，并且(A,C)可观测。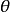是系统的未知参数向量；d (t)，D(t)为有界外界扰动。

不确定混沌系统的自适应同步不确定混沌系统的自适应PID同步PID控制方法是自动控制领域中应用最为广泛的经典方法，由于其算法简单且物理意义明确，便于调整参数，且具有良好的控制效果与鲁棒性，尤其是能够兼顾时域与频域的指标进行设计，因此受广大工程设计者青眯。邱道尹设计了一种基于单神经元的自适应PID控制系统，该系统具有响应平滑、无超调的优点，并对同一对象用常规PID进行控制，比较表明自适应PID控制系统具有自学习和自适应能力。徐峰基于蒙特卡罗实验原理，提出了一种针对适应型PID控制器的参数整定比较方法。赵建华将现代控制理论的自适应技术与经典的PID控制算法相结合，推导出一种自适应 PID控制算法，并应用于不同对象进行仿真验证。李亮提出一种可变参数的自适应PID控制方案应用于汽车牵引力控制系统，根据驱动轮实际滑转率的偏差自适应调整PID控制器中的整定参数，从而改善PID控制的控制品质。

在实际过程中，被控过程经常存在时变不确定性的特点，自适应PID控制是解决这一问题的有效途径。因此本文从PID控制入手研究，由于混沌同步系统的不确定性，考虑采用自适应算法，针对不确定性抽象后的数学有界模式，研究不确定混沌系统的自适应控制与PID控制的复合控制算法，理论研究与数字模拟仿真表明该方法能够合理有效的继承传统PID控制算法与自适应算法的优点，具有很好的同步效果。

不确定混沌系统的鲁棒自适应同步鲁棒控制是处理不确定性的一种强有力的手段，在近二十年得到充足的发展。而自适应控制与鲁棒控制在很多系统中匹配应用，相互相辅相成不可或缺，确定了单独鲁棒控制与自适应控制所无法得到的良好效果。侯砚泽针对切换信号依赖于独立决策变量的不确定切换系统，基于多Lyapunov函数方法和模型参考自适应控制理论，提出并分析一种控制器具有非线性死区特征的鲁棒自适应切换控制方案，仿真结果表明系统在快速连续切换下可良好地跟踪期望轨迹。柯海森对一类满足匹配条件的输入干扰不确定非完整的约束移动机器人，借助无源化方法提出了一种饱和鲁棒自适应控制器，该控制器能够不需要事先确定未知干扰的上界值。关新平研究了两个混沌系统都存在扰动情况下的鲁棒自适应同步问题。该方法能有效地克服不确定性对同步所造成的破坏;实现了良好的同步效果。并针对Lorenz系统进行了数值计算，数值计算结果证明了所给方法的有效性。王宏伟利用Lyapunov稳定性定理确定正交函数神经网络控制器的权值更新规则，并保证权值误差和跟踪误差的有界性，提出了基于Chebyshev正交函数神经网络的不确定性混沌系统的鲁棒自适应同步方法。该方法能克服不确定性对混沌系统同步的破坏，实现了良好的同步效果。

通过上一节的自适应PID同步控制规律研究可以看出，针对不确定性的假设给控制律设计带来了复杂度，为了进一步简化自适应PID复合同步规律的设计，考虑对模型不确定性进行抽象简化，以便于采用鲁棒控制方法处理不确定性。因此针对模型不确定性考虑提出相对误差状态一阶有界的假设，而由于混沌系统的有界性，使得其容易被一般混沌系统所满足。1

不确定混沌系统的极点自调节同步极点配置是经典状态反馈控制研究中非常重要的思想，其物理意义非常明确。尽管极点配置的提出首先是针对线性系统的传递函数模型，进一步也可以沿用到线性系统的状态空间分析中，但其仍然能被有效应用于非线性系统的局部线性化控制中。通过配置具有远离虚轴的系统极点，一方面能够保证系统具有快速的响应速度，另一方面能够保证系统具有一定的抗干扰能力与鲁棒性。而由于混沌系统的有界性，尽管在混沌系统非线性的影响下，不难推断存在足够大的理想线性状态反馈规律，使得混沌系统的同步能够实现。方敏提出一种新颖的极点配置自调节算法，该算法在配置闭环极点的同时，对调节器的高频增益加以限制，以减弱控制信号的高频振荡。单剑锋对于一大类时滞最小相位二阶系统，设计了一种基于相消原理极点配置自校正PID调节器，该方法具有计算简单，收敛快，鲁棒性好的优点。Alban Puai较早地研究了采用极点配置的方法来实现混沌系统的同步。Li Cheng 随后研究利用控制理论中的极点配置方法，解析分析了离散超混沌系统同步与控制的条件，其同步与控制方案均采用单路组合信号反馈的形式。

不确定混沌系统的有限时间滑模同步控制近年来，在非线性领域中，混沌同步研究己经引起了学者们的广泛关注。由于混沌系统对初值和参数变化的极其敏感性和随机性，以至于混沌同步在保密通信、生物工程，信息处理等学科范围内得到广泛的应用。在众多的同步控制策略中，因为滑模控制对系统中存在的一些不确定因素具有很强的鲁棒性，对参量变化不敏感性以及设计简单等优点，近年来得到了很多的关注与研究。在工程应用中，混沌系统的参量可能在某些范围内波动，因为它一定会受到外界环境的干扰，所以系统中参量不可能完全可知。因此，对带有未知参量的混沌系统同步的研究非常有实际价值，针对系统中的未知参数，学者们提出了自适应方法进行在线估计。除了未知参数对系统影响，由于受到激励的限制，在设计控制律的过程中非线性输入对系统的影响也不可忽略。然而，在实际工程应用中，系统中的未知参数、非线性输入、不确定性以及外部扰动等诸多的因素都会限制和影响控制器的使用。

不确定混沌系统的鲁棒自适应容错同步控制在探讨和分析混沌同步的情况时，学者们大多将重点放在混沌系统无故障的情况，来设计合适的控制器进行同步控制。然而，在实际应用的过程中，传感器、执行机构和系统内部元件都存在产生故障的可能性，发生故障时传统的控制方法就会失效，破坏了两个系统之间的混沌同步。混沌同步广泛地应用在保密通信中，为了保证通信质量，设计一个可靠的容错控制器，使当有故障发生时，仍能保证两个系统之间达到同步是非常必要的。

学者们很快开始了对容错控制的研究。容错控制大体可以分为两类，即被动容错方法和主动容错方法。被动容错控制的思想是不需要调整控制器参数及结构，结合鲁棒控制方法使得闭环控制系统对出现的故障并不敏感，即使有故障发生时，系统仍能正常运行并能满足规定的性能指标。但控制器的设计保守，所达到的控制效果不能令人满意。主动容错控制方法可以有效的解决上述问题。主动容错控制的策略是系统一旦产生故障就要改变控制器的参量或结构，来保证系统的稳定运行。到目前为止，国内外针对混沌同步的容错控制的相关研究成果却很少，因此，在本章中以带有执行器故障、外界干扰以及非线性不确定性的混沌系统作为被控对象，提出一个鲁棒自适应容错控制策略，即使系统有故障发生时，仍能完成两个混沌系统的同步控制。2