[科普中国]-流动理论

简介

流动理论假设材料的徐变与粘滞流动具有某种相似的性质，认为徐变的应变速率与应力、时间之间存在着某种简单的函数关系，即：

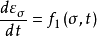
以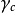、 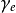和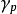 表示徐变应变速率、弹性应变速率和塑性应变速率，由此得到总的应变速率为：

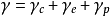
当应力未超过弹性极限时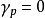，，弹性应变速率为：

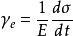
试验发现，当工作温度不变时，金属材料在缓慢并单调变化的应力作用下，徐变的应变速率可表示为：

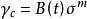
式中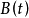，等于单位应力作用下的徐变速率。

由此可得总应变速率为：

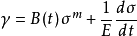
在上式中，当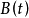为常数且m=1时，可得到Maxwell方程，故流动理论方程是Maxwell方程的普遍形式。

当时间很长时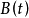，接近于常数B，如果载荷不变且可以略去微小的弹性应变速率，则采用更为简单的流动理论规律：

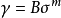
这一方程描述了物体非线性粘滞流动的性质。1

应用范围与特点流动理论在应用上具有与老化理论相似的限制：在应力为单调而且缓慢变化的情况下，流动理论是适用的1。流动理论方程明显地包含时间因素，起始时刻若有变化，则流动理论的方程也相应变化。2

流动理论与形变理论流动理论与形变理论之间存在一定的关系。在简单加载条件下，从流动理论可以导出形变理论，简单加载下形变理论与流动理论是一致的。在加载路径偏离简单加载不大时，由形变理论得到的结果也与流动理论相差不多。3