[科普中国]-椭圆参考轨道

简介

椭圆参考轨道相对运动的控制技术是空间相对运动控制技术发展的趋势。在已经工程实现的自主交会对接中，目标飞行器几乎都运行在圆轨道或者近圆轨道上，而有关编队飞行的研究大部分集中在圆参考轨道编队，随着航天工程技术的进一步发展，椭圆参考轨道相对运动的控制技术成为空间活动必需的基础技术，对其需求体现在三个方面:(1)椭圆参考轨道的交会与编队；(2)空间在轨服务；(3)空间攻防。椭圆参考轨道相对运动的动力学分析为交会制导、编队队形设计、抑制相对‘运动漂移提供理论基础，相对运动的控制技术为工程实现椭圆参考轨道附近的交会与编队提供技术方案，椭圆参考轨道编队的工程实践对相对运动的动力学分析和控制技术提出更高的要求。空间在轨服务技术能够实现燃料加注、载荷装配、在轨检查和维修等后勤服务，是一项无法替代的关键技术，曾在多次航天活动中发挥重要作用:(1)利用挑战者号航天飞机对SMM卫星实施在轨维修和部件更换；(2)维修和释放Syncom IV卫星；(3)更换Intelsat6-F3卫星的发动机并重新释放该卫星；(4)五次维修哈勃太空望远镜;(5)建设国际空间站ISS。空间在轨服务技术的发展对相对运动控制提出了更高的要求，如XSS实验卫星系统项目和Orbital Express轨道快车项目需要实现交会、伴飞、绕飞、捕获、对接等技术，因而椭圆参考轨道相对运动的控制技术成为进一步发展空间在轨服务所需的基础技术。美国和俄罗斯在空间攻防领域的快速发展导致反卫星武器、轨道武器、轨道转移飞行器(OTV)等军事航天器的不断出现，此类航天器对其他国家的空间资产构成巨大威胁，美国X-37B轨道机动飞行器的两次成功升空加剧了各国对空间资产安全的担心。为了应对此类威肋、而发展天基平台实现对敌对航天器的拦截、监测、捕获等操作，椭圆参考轨道相对运动的控制技术是必不可少的。

椭圆参考轨道的相对运动控制成为近期的研究热点。对近地空间飞行器相对运动近半个世纪的研究主要集中在圆(近圆)参考轨道的交会对接、圆参考轨道的编队飞行和椭圆参考轨道的最优线性化交会上，考虑非线性和摄动影响的椭圆参考轨道相对运动控制技术则是近十年来的研究热点。1

水平圆构形编队周期性绕飞的编队构形设计，在编队卫星技术的具体应用中具有十分重要的作用。传统的方法是基于Hill方程或Clohessy Willshire方程(简称HCW方程)进行编队卫星构形设计。HCW方程是一组常系数的线性微分方程，具有简单的解析解，通过对HCW方程解析解的分析，可直观的设计一些较典型的编队构形，其中水平圆是引起广泛关注的构形之一。水平圆是指环绕卫星相对参考卫星的运动轨迹在水平面内投影为圆的周期性绕飞构形，这种构形在对地观测中具有较好的特性，成为许多对地观测任务首选的构形。

传统的基于HCW方程的水平圆构形设计是以参考轨道为圆轨道为前提的，基于圆参考轨道的假设限制了水平圆构形编队的应用范围。李海阳研究了基于一般开普勒参考轨道水平圆构形的设计问题，重点讨论了椭圆参考轨道水平圆构形的设计和演化，分析了椭圆参考轨道水平圆编队构形的特点。首先以作者提出的利用能量守恒原理确定的椭圆参考轨道周期性绕飞条件为约束，给出了类似HCW方程的椭圆参考轨道周期性相对运动的解析解;其次通过对解析解的直观分析，提出了椭圆参考轨道水平圆构形的设计方法，研究了水平圆构形的演化;最后通过数值仿真验证了设计方法的正确性。2

最优精确交会在Hill给出的月球相对于地球的相对运动动力学方程的基础上，Clohessy和Wilts hire给出了描述圆参考轨道相对运动的C-W方程。不久之后，Tschauner和H empel给出了描述椭圆参考轨道相对运动的T-H方程。此后，C-W方程被广泛地应用于空间交会对接的研究和工程实践。编队飞行概念的提出使得相对运动动力学的研究再次成为热潮。C-W方程和T-H方程都是在地球为球形、相对运动距离远小于参考轨道半径的假设下线性化引力场得出的，没有考虑地球非球形摄动的影响。因此这类方程及其改进形式给出的解析结果不适用于考虑地球扁率的影响且相对距离较大的相对运动。

对于地球扁率和其他轨道摄动源对参考星轨道和追踪星轨道的影响，很多学者给出了考虑不同程度摄动的结果。Kechichian考虑大气阻力和地球扁率的影响给出了一组非线性动力学方程，该方程可以精确描述大气阻力及地球扁率对相对运动的影响。Gim和Alfriend采用几何化方法给出了轨道要素差到直角坐标相对运动状态的状态转移矩阵(轨道要素差可由平均轨道要素或密切轨道要素表述)该状态转移矩阵考虑了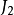摄动对目标星和追踪星轨道要素长期项的影响。Sengupta、Vadali及Alfriend采用平均化思想，考虑了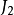摄动对目标星和追踪星轨道要素长周期项和短周期项的影响，给出了平均化的相对运动的解析表达式。这些研究的共同特点是，相对运动动力学方程或其解的形式复杂，不利于制导律的设计。采用轨道要素差描述相对运动需要追踪星的轨道要素，而追踪星一般有变轨机动，对其轨道要素的测控有一定的难度。

圆参考轨道的交会问题已经取得了丰硕的研究成果，对于椭圆参考轨道交会问题的研究则主要集中在线性交会上，有关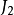摄动椭圆参考轨道非线性交会的文献较少。荆武兴等给出了两种易于实现的燃料最优寻优算法和一种考虑摄动影响的迭代交会制导算法，其中燃料最优寻优算法用来确定最优转移时间和最优双脉冲。另外还解决了半圈交会和整圈交会的最优双脉冲确定问题。考虑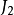摄动影响的椭圆参考轨道交会迭代制导算法采用线性梯度，其形式简洁易于实现。此迭代制导算法首先采用一种简洁的状态转移矩阵计算初始速度增量，然后利用考虑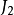摄动的精确非线性动力学方程传播追踪星相对于目标星的相对运动状态，最后根据终端交会误差利用线性梯度修正初始速度增量来提高交会精度。该迭代制导算法收敛快，适用于圆参考轨道和任意偏心率的椭圆参考轨道附近的远距离交会。3