[科普中国]-坡印亭定理

定理公式

电磁能量一如其他能量服从能量守恒原理，坡印亭定理用来表征电磁场能量守恒关系的。

积分形式的坡印廷定理对于由闭合曲面S所限定的体积V，有：

式中：J是电流密度；E是电场强度；H是磁场强度；B是磁感应强度；D电位移矢量

其中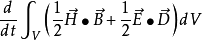： ——在单位时间内体积 V 内所增加的电磁场能量；

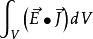——单位时间内电场对体积V中的电流所做的功，导电媒介中 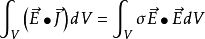即为体积V内总的消耗功率。

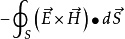——单位时间内通过曲面进入体积V的电磁能量

所以矢量ExH定义为电磁能流密度矢量S（坡印廷矢量），即

这样，若已知某点的E和H，即可求出该店的能流密度矢量。1

这就是电源外区域的、积分形式的坡印亭定理。它的含义是：垂直穿过闭合面S进入体积V的功率，等于体积内电磁储能的增长率与由传导电流J引起的功率损耗之和,更一般的情况是：

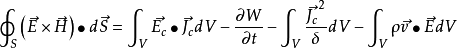
式中Ec为电源中的局外场强，Jc为传导电流，σ为体积V内介质的电导率，ρ为运动电荷的电荷密度，v为该电荷的运动速度，E=Jc/σ-Ee为总场强，W为 。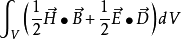

整个方程的含义是：外源提供的功率等于体积V内电磁能量的增加率、传导电流的功率损耗、运动电荷作功耗损的功率、垂直穿过曲面A向外界输送的功率之总和。

微分形式的坡印廷定理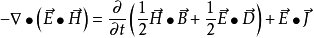

在体积V上，对上式两端积分，并应用散度定理，即可得到坡印亭定理积分形式。1

推导过程坡印亭定理可由麦克斯韦方程组推导出来。假设闭合面 S 包围的体积 V 中无外加源，媒质是线性的、各向同性的且参数不随时间变化。

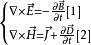分别用E 点乘方程[1]、H 点乘方程[2]，得

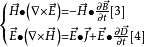将[3]、[4]两式相减，得到

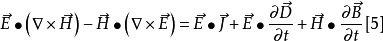在线性、各向同性的媒质中，当参数不随时间变化时

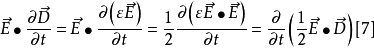
将[6]、[7]式代入[5]，于是得到，

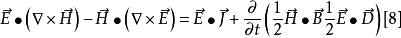
再利用矢量恒等式

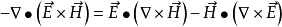
可得到

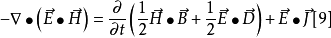
这就是坡印亭定理的微分形式，在体积 V 上，对[9]式两端积分，并应用散度定理，即可得到

这就是表征电磁能量守恒关系的坡印亭定理1

定理影响坡印亭定理给出了时变电磁场能量传播的一个新图像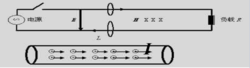，电磁场能量通过电磁场传播。这对广播电视、无线通信和雷达等应用领域是不难理解的。

恒定电流或低频交流电的情况下，场量往往是通过电流、电压及负载的阻抗等参数表现，表面上给人造成了能量是通过电荷在导线内传输的假象。

如果能量真的是通过电荷在导线内传输，常温下导体内的电荷运动速度约为10-5m/s，电荷由电源端到负载端所需时间约是场传播时间的亿万倍。

电磁场能量通过电磁场传播，负载只需通过极短（t=L/c，其中c为光速）的时间就能得到能量的供应。2