[科普中国]-完全可控性

可控性问题是现代控制理论与应用研究的一个基本内容。对于确定性线性系统，已有许多经典的结果。但是对于随机系统，可控性问题十分复杂，在概念上包含3个方面：完全可控、渐近可控和随机可控。1

可控性当系统用状态方程描述时，给定系统的任意初始状态，可以找到容许的输入量（即控制矢量），在有限的时间之内把系统的所有状态引向状态空间的原点（即零状态）。则系统是完全可控制的。如果只有对部分状态变量可以做到这一点，则系统不完全可控制。2

示例说明：

给定一个系统，输入是，状态变量是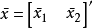，输出变量是：

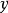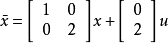
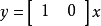
解：上述动态方程可写成：

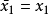
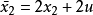
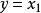由于输入不能控制状态变量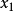，所以状态变量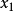是不可控的。2

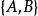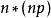状态的完全可控性判据1若定义连续时间系统的可控矩阵

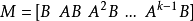
则系统状态完全可控（或系统可控）的充要条件是：该系统的可控性矩阵满秩，即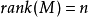

示例如下：

给定状态变量，试判别状态可控性。

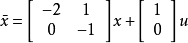
解：

该系统的可控性矩阵为：

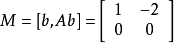
因为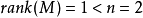，所以该系统不完全可控。2

判据2设连续时间系统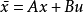 ，系统状态完全可控的充要条件为：当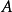为对角阵且特征根互异时，输入矩阵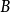无全零行。

示例如下：

（1）

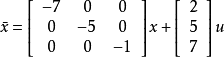
因为状态方程为对角标准型，且B阵中不含有元素全为零的行，故系统是可控的。

（2）

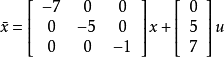
因为状态方程为对角标准型，但B阵中含有元素全为零的行，故系统是不可控的。2

判据3状态完全可控的条件也可用传递函数或传递矩阵描述。

状态完全可控性的充分必要条件是在传递函数或传递矩阵中不出现相约现象。如果发生相约，那么在相约的模态上，系统不可控。

示例如下：

给定传递函数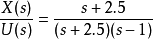：，判别系统的状态可控性。

显然，在此传递函数的分子和分母中存在相约的因子（s+2.5）（因此失去一个自由度）。由于有相约因子，所以该系统状态不完全可控。2

输出完全可控性设系统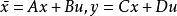，则系统输出完全可控的充要条件是：

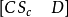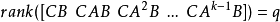输出可控性矩阵满秩，即其中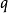， 为输出变量的个数。

一般而言，系统输出可控性和状态可控性之间没有什么必然的联系。即输出可控不一定状态可控，状态可控不一定输出可控。2