[科普中国]-非线性内模控制

与线性系统类似，非线性系统的内模控制结构如右图所示。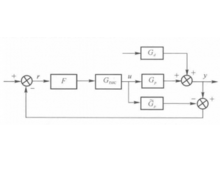

其中。Gp(s)为非线性对象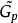，(s)为模型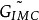，(s)为控制器，F为滤波器，Gd(S)为扰动或模型不确定因素。

可以证明，线性内模控制的三个重要性质均可以推广到非线性内模控制。但在非线性内模控制中，对象模型的获取和控制器的设计远比线性系统困难，利用经典的建模方法很难适应复杂非线性系统的建模需要。

系统的模型与对象并行运行，两者之间的输出误差经滤波器作用后反馈给非线性内模控制器，控制器从模型获取状态，并不需要得到对象的状态。若模型与对象完全匹配，且初始条件相同时，控制器将与传统非线性系统反馈线性化的结果一致。1

传统数学模型在内模控制中应用相当广泛，特别是以传递函数表示的输入、输出模型几乎统治了线性内模控制的研究。在非线性内模控制中，Henson(汉森)等研究了微分方程描述的仿射非线性对象和模型，Kendi(肯迪)等采用可因式分解的非线性算子研究存在可测干扰和输入饱和的仿射非线性系统。传统数学模型可逆性容易判断，模型可逆时能解析获得模型的逆，能够深入分析闭环系统的稳定性和鲁棒性，但是很多复杂非线性对象是难以用数学模型表示的。2

神经网络内模控制方法充分利用了神经网络强大的函数逼近能力，在一定程度上克服了非线性系统难以建模的困难，受到人们的青睐。

(1)神经网络内模控制一般采用以下两种方法：①两个神经网络分别逼近模型和模型的逆；②采用神经网络逼近模型，然后用非线性优化方法数值求取控制量。这两种方法固然可以获得较高精度的模型，但是模型逆的精度却往往得不到保证，这是因为获得的神经网络模型可能是不可逆的。

(2)根据内模控制的性质可知，当控制器偏离模型的逆使得控制器和模型的稳态增益乘积不等于1时，会导致控制系统跟踪阶跃输入出现静差，因此基于神经网络的内模控制需要解决以下理论问题：①以网络拓扑结构表示的神经网络模型如何判断其可逆性；②如果可逆，求逆的过程能否保证收敛；③能否求出一个高精度的模型逆。由此可见，非线性内模控制中模型可逆性的问题远比线性内模控制中的复杂。神经网络模型求逆的问题已经有一些数值算法，但是目前还缺乏严格的理论依据，因而在一定程度上限制了神经网络内模控制的应用。

由于模型逆的精度对内模控制效果的影响远大于模型精度所产生的影响，因此通过适当牺牲模型精度以确保模型可逆，并求得高精度的模型逆就成为解决非线性内模控制的一条可行之路。仿射模型的优点是模型逆可以解析获得，从而逐渐吸引了研究者的注意。其中采用仿射形式的Hopfield(霍普菲尔德)网络来逼近对象的方法，可利用该网络的稳定性定理判断模型和模型逆的稳定性；而另一种方法是基于双BP网络(多层前馈神经网络，Back Propagation network)组成的仿射模型，提出针对非线性离散时滞系统的神经网络内模控制器的设计。然而，这些方法的缺点是对一般非线性系统的建模精度不高，比较适用于仿射非线性对象。2

与神经网络相比，模糊系统的非线性函数逼近能力较晚为人们所认识，模糊模型最初应用于内模控制中所起的作用类似于神经网络输入、输出模型，因而也无法避免模型求逆的困难。但在Abonyi(奥博尼)和Edgar(艾德加)等的努力下，模糊模型求逆获得了较好的结果。Abonyi针对一类特殊的两输人一输出模糊系统提出了一种解析求逆的方法，并将结论推广到MISO模型。Edgar提出一种特殊的模糊模型，其建模过程可以保证模型总是可逆的，并能够在每个采样时间内获得精确的模型逆。另外，Fink(芬克)指出由于模糊系统建模过程是采用一系列线性模型加权平均来逼近非线性对象，因而模型求逆可以用局部线性模型求逆的加权平均来解析获得，使得求逆过程的计算量大幅减少。可以预见，由于模糊神经网络结合了神经网络和模糊逻辑二者的优点，具有自学习和利用知识的能力，在一定情况下还可以解析获得模型逆，因此作为内模控制建模工具的研究潜力很大。2

Volterra(沃尔泰拉)级数模型是一种重要的非线性系统模型，可以描述一大类工业对象。作为一种非参数模型，该模型的优点是可以通过系统输入、输出数据直接辨识得到，而不需要复杂的结构辨识过程。不过从模型辨识的角度看，Volterra级数需要相当多的被估计参数才能取得满意的精度，这在很大程度上限制了这种方法的应用。2

非线性内模控制有机地结合了非线性反馈线性化技术与内模控制结构，系统不但对模型失配、参数变化及各种不确定性干扰具有强鲁棒性，消除不确定性的影响，而且能够很好地补偿被控对象的非线性特性，从而取得优良的性能。3

但是众多的非线性内模控制方案很少应用于实际。实际控制时多采用计算机控制，需要将系统离散化，而离散化会带来许多意想不到的问题，比如离散化引起的误差若处理不当会对系统性能造成较大影响。2