[科普中国]-迭代函数系统

迭代函数系统

迭代函数系统（IFS）属于一种分形构形系统，是分形几何学的重要分支，借助计算机强大的迭代计算能力，将分形理论的精髓—自相似性、层次的多重性和不同层次的规则统一性，应用于计算机图形领域，可以产生许多具有无穷细节、精致纹理的图形。1

IFS是以仿射变换为框架，根据几何对象的整体与局部具有自相似的结构，将总体形状以一定的概率按不同的仿射变换迭代下去，直至得到满意的分形图形。

一个迭代系统由 个 维空间 上的仿射变换 组成，每个 对应的压缩比为 ，满足 ，且每个 有一个伴随概率 ， 且 。迭代系统IFS又记为： ，其中， ， 。由于主要在 空间考察 IFS，故可简记为 。

IFS 码是指 IFS 中的集合

拼贴定理设是完备度量空间上的IFS，压缩比为，变换由下式定义：

则是上压缩比为压缩映射，即，，且存在惟一的不动点（不变集），满足，并且对，有。

其中不动点 A 称为这个 IFS 的吸引子。IFS 的吸引子一般都是分形，称为确定性分形。从理论上讲，不管多么复杂的事物形态，只要能够确定其 IFS 代码就可以借助计算机再现事物的复杂形态。由拼贴定理可知，只要选择适当的仿射变换，就可以使得迭代产生的目标图像与分形图任意接近，所以 IFS方法在模拟分形图像方面具有极重要的意义。

绘制分形图形迭代函数系统绘制分形图形有两种方法：确定性迭代算法和随机性迭代算法。

确定性迭代算法确定性迭代算法是通过仿射变换得到的。其基本原理就是找一个初始集，对集上的每一个点，根据给定的仿射变换公式进行数据变换，便可得到新的点集。这样通过多次迭代，便可绘制所需的图形，并且每个图形的局部和整体相似。只要其仿射变换系数相同，即IFS码相同，当迭代次数足够大时，最终生成的图形是相同的。2

随机性迭代算法随机性迭代算法用到了概率，从而可以对图形的细节和颜色进行控制。随机性迭代算法的基本原理就是利用一个给定的 IFS 码（每一个仿射变换 对应于一个概率），从任选的一个初始点出发，依据其概率分布，从中选择相应的进行仿射变换，可得到新的点。然后，再由概率选择相应的进行变换，进而得到新的点。这样反复迭代，便可得到一系列的点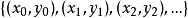。这些点集显示在屏幕上，便得到一个完整的分形图。2