[科普中国]-时变时滞系统

简介

从系统理论的观点看，任何实际系统的过去状态不可避免地要对当前的状态产生影响，即系统的演化趋势不仅依赖于系统当前的状态，也依赖于过去某一时刻或若干时刻的状态，这类系统称为时变时滞系统。时变时滞产生的原因有很多，如：系统变量的测量(复杂的在线分析仪)、长管道进料或皮带传输、缓慢的化学反应过程等都会产生时变时滞。时变时滞常见于电路、光学、神经网络、生物环境及医学、建筑结构、机械等领域，由于应用背景广泛，受到很多学者的关注。从理论分析的角度来看，在连续域中，时变时滞系统是一个无穷维的系统，特征方程是超越方程，有无穷多个特征根。而在离散域中，时变时滞系统的维数随时滞的增加按几何规律增长，这给系统的稳定性分析和控制器设计带来了很大的困难1。

特点时变时滞系统的特点是，其输出响应的波形不仅同输入波形有关，而且也同输入信号加入的时刻有关。这一特点增加了分析和研究的复杂性。对于时变时滞系统来说，即使系统是线性的，也只能采用时间域的描述。描述的基本形式是变系数的微分方程或差分方程。时变时滞系统的运动分析比定常系统要复杂得多。在工程中，应用最广的是所谓冻结系数法，这一方法的实质是在系统工作时间内，分段将时变参数“冻结”为常值，从而可分段地把系统看成为定常系统进行研究。通常，冻结参数法只对参数变化比较缓慢的时变时滞系统才有效。对时变时滞系统控制的一个可能的方案是，在采用估计器对参数进行在线估计的同时，采用适应控制系统实现控制2。

表示n维线性时变时滞系统的状态方程为：

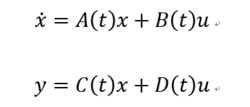
其中，u是p维输入向量，y是q维输出向量。A、B、C、D分别是线性系统的参数，均是时间t的函数，即参数随时间的变化而变化。

线性时变时滞系统的结构图如下：

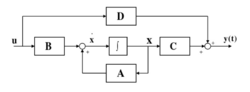
稳定性稳定性是设计控制系统的最基本要求。

线性时变时滞系统方程：

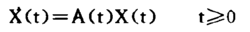
如果已经求出矩阵A(t)的所有特征值，系统渐近稳定的充要条件是：A(t)的所的特征值都位于S的左半平面。

展望由于时变时滞系统本身的复杂性，以及时变时滞特性的多元性和叠加性，致使这一研究领域中仍有大量的空白和难题没有涉及和解决。结合目前该领域的研究现，理论方法需要进一步完善的有：

1、“快”时变问题。针对更为一般的快时变时滞系统(如高阶线性快时变时滞系统、非线性快时变时滞系统等)，如何放宽现有方法对时变时间的要求，应用这些控制策略及算法进行实时的系统辨识与控制，或在此基础上作进一步的改进与更新等，尚有待更全面深入的研究。

2、系统的条件稳定问题。一般情况下，控制算法对于某一类时变系统而言都需要附加或多或少的稳定性条件或假设。针对此类问题，如何能够使这些为了保证系统稳定而提出的条件或假设不影响系统性能、产生尽可能少的限制。是将控制算法应用到实际控制过程的关键，因而具有非常重要的研究意义。

3、实时建模问题。建模的精确性与快速性通常对控制系统的性能具有直接影响，同时也关系到控制方法的可操作性。因此，若能够在时变系统的实时建模问题上进行深入研究，必将有利于时变系统控制方法的进一步应用与发展。

4、非线性问题。在非线性情况下，时变系统的微分方程的解析解往往不存在，甚至时变模型也不可得。如何利用现有的线性模型与时变系统控制方法。将其进一步推广至非线性系统，或者如何将非线性时变系统分段线性化，找出可与某些线性特性相替换的非线性特性，值得进行更加深入的讨论。

另一方面，从实际应用的角度,有以下几个问题需作进一步的探讨：

1、数据处理问题。对于实际过程中的动态数据需要进行适当的信号处理与分析，突出数据中的系统性信息，降低不相关的干扰噪声，在能够表征实际系统时变特性的基础上尽量降低系统复杂。

2、适用条件问题。在将理论方案付诸实践时，需要事先对实际的时变对象作出准确判断，根据具体情况选择适用的解决方案，必要时还要对理论方法作些灵活的调整甚至改进。

3、时变因素的不确定问题。由于实际系统往往复杂多变,存在大量的不确定因素，为节省研究成本并提高工作效率，可以采取仿真实验与实际相结合的方法，必要时甚至需要设定多种控制方案。同时对实际系统的时变环境也要有足够的了解，在仿真实验时需对控制方法进行尽可能全面的可行性讨论，在实际应用时再进行准确快速的调整。