广义预测控制(GPC)是随着自适应控制的研究而发展起来的一种预测控制方法。 它采用了大范围滚动预测, 能够获得更多被控过程的动态信息,还能通过对模型的在线辨识,以适应单元机组动态特性的变化, 计算出合理、 优化的控制信号, 呈现良好的控制性能和鲁棒性, 适用于控制不易建立精确数学模型的工业生产过程。 对于多输入多输出系统, 由于系统内部的相互耦合给系统控制带来了困难,要想取得满意的控制效果,就要研究多变量系统的解耦问题。1
设计方法被控过程的数学模型采用下列具有随机阶跃扰动非平稳噪声的离散差分方程描述:
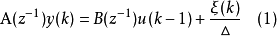 其中,
其中,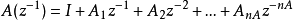 ,
,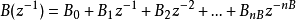
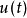 和
和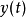 为
为 维输出向量,
维输出向量,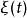 是均值为零、方差为
是均值为零、方差为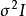 的白噪声。 并假设
的白噪声。 并假设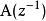 为一对角矩阵。
为一对角矩阵。
将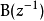 分为两部分:
分为两部分:
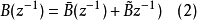
其中,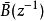 是一个对角矩阵多项式,
是一个对角矩阵多项式,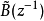 是一个对角线为零的矩阵多项式。可以看出,
是一个对角线为零的矩阵多项式。可以看出,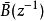 是输入输出之间的直接联系,
是输入输出之间的直接联系,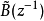 是通道之间的相互耦合部分。
是通道之间的相互耦合部分。
式(1)可以改为:
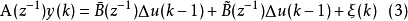 其中,
其中,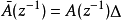 ,
,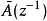 也是对角矩阵。
也是对角矩阵。
定义Diophatine方程:
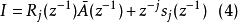 其中,
其中,
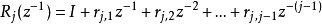
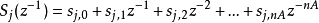
因为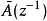 是对角矩阵,所以
是对角矩阵,所以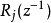 和
和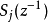 也是对角矩阵。
也是对角矩阵。
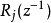 左乘式(1),并化简得:
左乘式(1),并化简得:
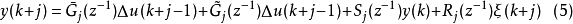
其中,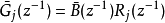 ,
,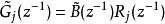
显然,上式的前三项和第四项不相关,则 j 步导前最优预测为:
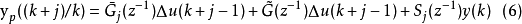
其中,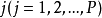 为预测步数,P为最大预测长度。
为预测步数,P为最大预测长度。
将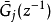 和
和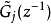 分别分为两部分:
分别分为两部分:
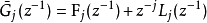
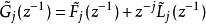 其中,
其中,
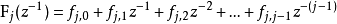
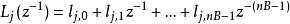
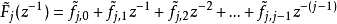
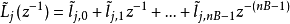 则优化算式可以改写为:
则优化算式可以改写为:

控制性能指标选取如下:
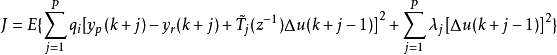
其中,M 为控制时域长度;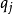 和
和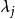 为输出预测误差和控制增量加权系数,都是对角矩阵;
为输出预测误差和控制增量加权系数,都是对角矩阵;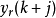 为参考输入轨迹。同一般的广义预测控制性能指标相比, 式中多出一项
为参考输入轨迹。同一般的广义预测控制性能指标相比, 式中多出一项 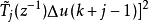 ,主要是用来消除各通道之间的耦合作用。1
,主要是用来消除各通道之间的耦合作用。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国