在概率统计理论中,随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布的,这些变量称为独立同分布变量。1
性质:
(1)服从同一分布
(2)相互独立
随机变量以一维随机变量为例:
观察一个随机现象,其样本点可以是具有数量性质的,也可能是非数量性质的,前者如抛一枚骰子,可能出现的点数是1点、2点、...、6点;后者如掷一枚硬币,可能出现正面,也可能出现反面,现在约定:“出现正面”记为1,“出现反面”记为0。无论是哪一种情形,都体现出这样的共同点:对随机试验的每一个可能结果,有唯一一个实数与之对应。这种对应关系实际上定义了样本空间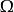 上的函数,
上的函数,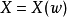 ,
,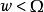 。
。
设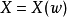 是定义在样本空间
是定义在样本空间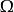 上的实值单值函数,称
上的实值单值函数,称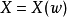 为一维随机变量。随机变量,通常用大写字母 X,Y,Z,W,...表示1
为一维随机变量。随机变量,通常用大写字母 X,Y,Z,W,...表示1
在概率论中,相互独立,是设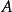 、
、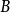 是两事件,如果满足等式
是两事件,如果满足等式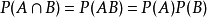 ,则称事件
,则称事件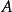 、
、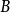 相互独立,简称
相互独立,简称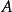 、
、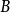 独立。
独立。
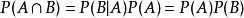
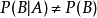 设
设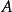 、
、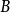 是试验
是试验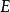 的两个事件,若
的两个事件,若 ,可以定义
,可以定义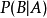 。一般,
。一般,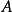 的发生对
的发生对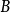 发生的概率是有影响的,所以条件概率,而只有当
发生的概率是有影响的,所以条件概率,而只有当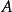 的发生对
的发生对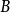 的发生没有有影响的时候才有条件概率
的发生没有有影响的时候才有条件概率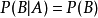 。这时,由乘法定理。
。这时,由乘法定理。
注:若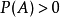 ,
,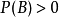 ,则
,则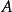 、
、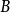 相互独立与
相互独立与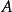 、
、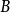 互不相容不能同时成立,即独立必相容、互斥必联系。
互不相容不能同时成立,即独立必相容、互斥必联系。
推广:
设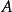 、
、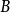 、
、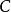 是三个事件,如果满足
是三个事件,如果满足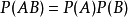 ,
,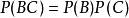 ,
,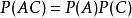 ,
,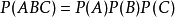 ,则称事件
,则称事件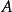 、
、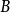 、
、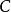 相互独立。
相互独立。
更一般的定义是,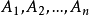 是
是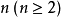 个事件,如果对于其中任意2个、任意3个、…、任意n个事件的积事件的概率,都等于各个事件概率之积,则称事件
个事件,如果对于其中任意2个、任意3个、…、任意n个事件的积事件的概率,都等于各个事件概率之积,则称事件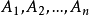 相互独立。1
相互独立。1
(1)均匀分布
设连续型随机变量 X 具有概率密度
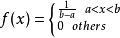 则称 X 在区间(a,b)上服从均匀分布,记为
则称 X 在区间(a,b)上服从均匀分布,记为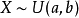
(2)指数分布
设连续型随机变量 X 具有概率密度
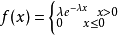
其中,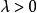 为常数,则称 X 服从参数为
为常数,则称 X 服从参数为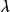 的指数分布
的指数分布
(3)正态分布
设连续型随机变量 X 的概率密度为:
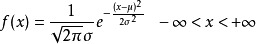 其中,
其中,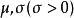 为常数,则称X 服从参数为
为常数,则称X 服从参数为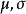 的正态分布。1
的正态分布。1
已知随机变量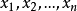 相互独立且同分布,方差为
相互独立且同分布,方差为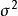 ,
,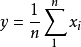 ,求
,求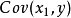 。1
。1
解答:
设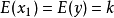 ,则有
,则有
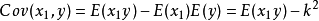
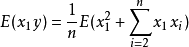
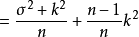 将下面的式子带入,很容易得到:
将下面的式子带入,很容易得到:




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国