[科普中国]-递阶模糊系统

模糊控制领域已经从简单的系统发展到更复杂系统，随之而来的问题是：模糊控制器的规则随着输入变量数量呈指数增长，在实际应用中要求很大的内存，并且难以在实际应用中实现。递阶模糊系统是解决这个“规则爆炸”问题的有效方法，它用递阶的形式将几个维数很少的模糊系统连接起来，从而达到大大减少规则库内规则数量的问题。递阶控制的基本原理是把一个总体问题分解成有限数量的子问题。对于复杂的系统，通常采用多级金字塔式的递阶控制结构1。

递阶模糊系统的结构形式很多，可以是多个低阶模糊系统以任何递阶形式相连。可以采用不同的方法随机生成具有任意输入变量个数的子模糊系统，构成递阶模糊系统。这是进行递阶模糊系统研究的一个方向。也可以选择双输入二层递阶模糊系统，然后进行结构辨识和参数辨识。我们知道当各级子模糊系统只有两个输入时，总规则数目最小。

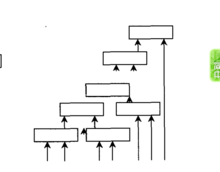
举一个递阶模糊系统的典型例子：每个子模糊系统都只有两个输入与一个输出，输出与另一个输入变量共同输入到下一个子模糊系统中，直到最后一个输入变量。

在这种结构的系统中，若对每个输入变量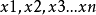 。和中间变量 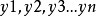。进行m个划分，则总的规则条数为 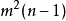。对比在传统通用的模糊系统，其总的规则条数为 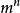，可以看出前者仅是输入变量个数n的线性函数，而后者却是n的指数函数，显然前者要小得多，大大减少了规则数。

递阶模糊系统的结构辨识必须解决每一级子系统输入变量的配置问题。在实际的问题中，我们知道其中的某些变量比其它变量更重要，对输出的影响更大。例如变量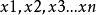 通过不同的二维模糊子系统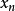，只是通过一个模糊子系统；而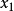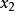，则通过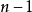个模糊子系统。所以实际的问题是将重要的变量放在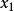或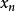。为了回答这个问题，必须知道输出是对哪一个变量更敏感。在参数辨识阶段，将每一级子系统的希望输出均设定为最后系统的输出，然后从第一级开始逐级进行参数的优化。应当将最重要的输入变量配置在第一级，较不重要的放在下一级等等。因此就要对每一个输入变量的重要性进行排序。

通常我们从要辨识的系统中只能得到许多输入输出量，而没有其它的信息，如何辨识模糊模型的初始结构就变成重要的问题。聚类的目的就是从大量的数据中提取固有的特性，从而获得系统行为的简洁表示。它不仅广泛的应用于数据的组织和分类，而且在数据压缩和模型构造方面有用处。常见的聚类方法均值聚类、分层聚类、模糊聚类、减法聚类方法等。

在将传统的模糊系统转化为一般类型的递阶模糊系统时，除了考虑规则爆炸外，还有就构成递阶模糊系统模糊化，去模糊化所用到的加法器，乘法器，减法器，比较器除法器等)所需要电子元件而言的计算复杂度以及运算时间等问题。

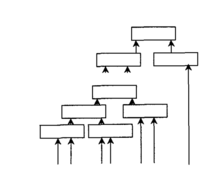
在构造递阶模糊系统时，有时系统输入变量中的几个是相关的，通常要将其尽可能地放在同一层。对于具有最小完备规则库的递阶模糊系统来说，可以选择另一种结构的系统这两种特殊结构的递阶模糊系统，如下图所示同样是具有最小完备规则库的。虽然这两种系统都是根据最优化规则库原则设计，但在实际应用中使用者要根据情况选择，并适当修改结构。左图为输入变量是偶数，右图为输入变量是奇数。