[科普中国]-韦格纳分布

数学定义

韦格纳分布函数有几个不同的定义。这里给出的定义特定于时频分析。给定时间序列x [t]，其非稳态自相关函数由下式给出

然后通过以平均时间表示自相关函数给出t=(t1+t2)/2和时间滞后 =t1-t2，傅里叶变换滞后。

因此，对于单个（平均零）时间序列，韦格纳分布函数简单地是

韦格纳分布函数的功能是随时降低光谱密度函数t，对于固定过程，完全等同于非平稳自相关函数。因此，韦格纳分布函数告诉我们（大概）频谱密度如何随时间变化。

交叉项干扰韦格纳分布函数不是线性变换。当输入信号中存在多于一个分量时，会发生交叉项（“时间跳动”），与频率跳动相似。该时频分布是双线性的，对于多分量信号而言，韦格纳分布存在严重的交叉项干扰。相比之下，短时傅里叶变换没有这个特征。韦格纳分布的负特征反映了经典信号的伽柏极限，与物理上与量子结构的任何可能的底层无关1。

以下是展示韦格纳分布函数的交叉干扰的一些示例。

为了减少交叉干扰，已经提出了其他几个变换，包括修改的韦格纳分布函数，伽柏-韦格纳变换和科恩类分布。

性质韦格纳分布函数具有下面列出的几个明显属性。

投影属性

恢复属性

时刻属性

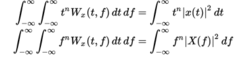
区域属性

乘法定理

卷积定理

时变协方差

时间-频率分析示例以下是一些示例，说明如何在时间 - 频率分析中使用韦格纳分布。

恒定输入信号当输入信号恒定时，其时间 - 频率分布是沿着时间轴的水平线。例如，如果x（t）= 1，那么

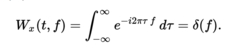
当输入信号为正弦函数时，其时频分布是与时间轴平行的水平线，由正弦信号的频率偏移。

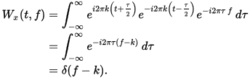
德尔塔输入信号当输入信号为增量函数时，由于在t = 0时它只是非零，并且包含无穷大的频率分量，所以它的时间 - 频率分布应该是跨原点的垂直线。这意味着delta函数的时间频率分布也应该是delta函数。由韦格纳分布可知

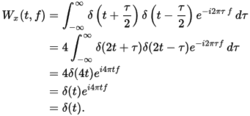
当输入信号的相位为二阶或更低时，Wigner分布函数最适合于时间 - 频率分析。对于这些信号，韦格纳分布可以精确地产生输入信号的时间频率分布。

优缺点优点：

1.有良好的分辨率，尤其是对单一成分，且瞬时频率变化不为2次式以上。

2.有好的数学运算性质。

3.可用于分析随机程序。

缺点：

1.有相交项(cross term)的问题。

2.需要更多的时间去计算，若讯号时间越长，则需要更久的时间。

3.不是一对一函数，无法辨别相位部分。

4.不适合分析瞬时频率变化为2次式以上的型态。