[科普中国]-分层图像表示

计算机视觉在本质上式计算代价十分昂贵的，仅考虑所需处理的巨大数据就会得出这个结论。因为我们想要实现视频或交互性的系统，所以期望得到非常快的响应。一种方法是使用并行计算机(强力)。不幸的是，很多计算机视觉问题都很难在多处理机间分配计算负担，或者根本无法分解。分层数据结构使得使用一些特殊算法成为可能，这些算法在相对小的数据量的基础上决定处理策略。它们使用知识而不是强力来减轻计算负担，并提高处理速度，只对图像的实质部分才在最精细的分辨率上工作。

金字塔和四叉树是两种典型的图像的分层数据结构。1

金字塔属于最简单的分层数据结构，主要存在有两种结构：M型金字塔（M-pyramids，矩阵型金字塔）和T型金字塔（T-pyramids，树型金字塔）。

M型金字塔是一个图像序列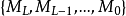 ，其中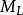， 是具有与原图像同样的分辨率和元素的图像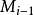， 是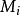 降低一半分辨率得到的图像。当创建金字时，通常只考虑维数时2的幂的方阵，这时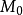， 则仅对应于一个像素。

当需要对图像的不同分辨率同时进行处理时，可采用M型金字塔。分辨率每降低一层，数据量则减少4倍，因而处理速度差不多也提高4倍。

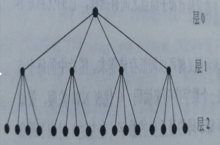
通常同时使用几个分辨率比仅使用M型金字塔中的一个图像要优越。对于这类算法，一般更喜欢用T型金字塔，树状结构。

设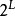是原始图像的大小（最高分辨率），T型金字塔计算如下：

1）一个结点集合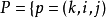，使得级别 ；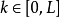

2）一个映射 F，定义在金字塔的结点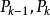之间，

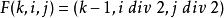其中，div表示整除

3）一个函数 V ，将金字塔的结点P映射到Z，其中，Z是对应于亮度级别数的所有数的子集合，例如， 。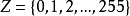

对于给定的k，T型金字塔的结点对应于M型金字塔的一些图像点，结点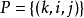集合的每个元素对应M型金字塔的一个矩阵，称k 为金字塔的层数。对于给定的k ，图像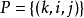构成金字塔第 k 层的一个图像。F是父亲映射，在T型金字塔中，除了根（0，0，0）之外的所有结点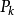都有定义。除了叶子结点外，T型金字塔的每个结点都有4个子结点；叶子结点是第L层的结点，对应于图像的单个像素。

T型金字塔单个结点的数值由函数V定义。叶子结点的值就是原始图像在最高分辨率下的图像函数的值（亮度），图像的尺度是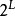。树的其他层结点的数值或者四个子结点的算术平方根，或者由粗采样定义的值，意味着使用的是一个子结点的值（比如，左上）

M型金字塔存储所有图像矩阵所需要的像素的个数为：

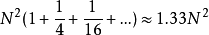其中，N 是原始矩阵（最高分辨率的图像），通常是2的幂。

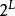T 型金字塔夫人存储表示与M型金字塔相似。树的弧不必存储，这是因为由于其结构的规范性，树的子结点和父结点的地址都很容易计算出来。1

四叉树是对T型金字塔的改进，除叶子结点外，每个结点由4个子结点。与T型金字塔相似，在每个层次图像被分解为4个象限，但无须在所有层次上保留结点。如果父节点有4个具有相同值（亮度）的子结点，则无须保留这些子结点。对于具有大的均匀区域的图像来说，这种表示比较节省。

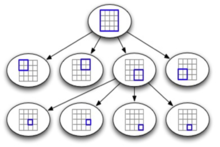
用四叉树来表示图像的优点是，对于图像相加、物体面积计算和统计矩计算存在简单的算法。四叉树和金字塔分层表示的主要缺点是，它们依赖于物体的位置、方向和相对大小。两个仅有微小差别的相似图像可能会具有非常不同的金字塔或四叉树表示。甚至，当两个图像描述的是完全相同而只是略微移动了的景物时，也可能产生完全不同的表示。

这些缺点在使用规范的形状四叉树时可以避免，这时我们并不给整个图像建立四叉树，而是给一个个物体建立四叉树。这种表示要用到物体的几何特征包括质心和主轴，首先得到每个物体的质心和主轴，然后找到中心在质心而边平行于主轴的最小外接矩形。最后将这个矩形（子图象）用四叉树来表示。用规范的形状四叉树和若干附加的数据项（质心的坐标、主轴的角度）表示的物体具有平移、旋转和尺度不变性。

四叉树已有广泛的用途，特别是在地理信息系统领域，与其在三维空间中的推广“八叉树”一起，在迭层数据的分层表示方面已被证明是十分有用的。1

金字塔结构使用非常广泛，有几个扩展和修正。

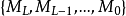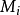一个简单的M型金字塔是一个图像序列，其中， 是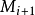 的2×2缩影。定义“缩影窗口”的概念，对于 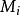的每个单元c ，它的缩影窗口 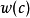是它在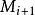 中的孩子的集合。在这里，一个单元 c 是图像 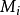在相应金字塔分辨率层次下任何单独的元素。如果图像的创建方式使得所有的内部单元都具有相同数目的邻居，而且，它们具有相同数目的孩子，那么这样的金字塔就是规范的。

可以用缩影窗口和“缩影因子”来建立规范金字塔的分类标准，缩影因子定义了层间的图像区域的降低比率：

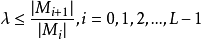在最简单的情况下，缩影窗口是2×2的且互不重叠，此时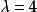。若选择让缩影窗口有重叠，缩影因子就会降低。表征规范金字塔的符号是（“缩影窗口”）/（“缩影因子”）1