[科普中国]-渐近无偏估计量

定义

渐近无偏估计量是随着样本容量n增加趋于无偏的参数估计量。

设总体X的分布函数为 是未知参数θ的一个估计量，若则称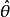 是θ的渐近无偏估计。如样本方差 是总体方差的渐近无偏估计，但并非无偏估计，因为它的数学期望为。

无偏性与渐近无偏估计量由于样本的随机性，对于个别样本，其估计值可能偏大或偏小。但从平均值来看，一个好的估计量应该等于被估计参数。即作为一个随机变量，它所取的值应集中在未知参数的真值或均值附近。

如果估计量的均值(数学期望)等于被估计参量(一般为随机变量)的均值(数学期望)，则称此估计量具有无偏性，为无偏估计量，数学表达式为

若被估计参量为确定的，即，则无偏性可表示为

若满足关系式(其中n 为样本数)，则称为渐近无偏估计量。

无偏性是一个所期望的性能。但一般情况下，渐近无偏估计量也是非常有用的2。

例题分析现在来考虑一个线性平稳过程的自相关函数的两种估计量。

假定数据是独立观测的，容易看出，是的一个无偏估计量，而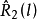是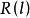的有偏估计量，因为

可以看到是有偏的，但它是渐进无偏的，即

若不等于则称为有偏估计量，差值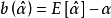称为估计量的偏差或偏量。

估计量的无偏性保证了估计值分布在被估计量的真值或均值附近2。