[科普中国]-非线性PID控制

简介

传统的PID控制是误差的比例、积分、微分三项的线性组合，它具有原理简单、参数易于调整、鲁棒性较强等特点，在工业过程控制中得到了广泛的应用。但是对于一些复杂的系统，特别是非线性对象，PID控制器并不能得到满意的效果。如果对传统的PID加以改进，使其能对一些非线性对象实现较高的控制要求，将有很大的实际意义。非线性PID是在传统PID的基础上引进非线性因素来加以改进的，控制量的基本要素不是直接取自输入-输出的误差，而是经过非线性变化后的误差的比例、积分和微分。由于非线性PID控制器中的增益参数能够随控制误差而变化，从而克服和减弱了非线性因素的影响，提高了控制器的鲁棒性和适应性1。

结构原理图图1是非线性PID控制器的结构原理图。图中，r(t) 为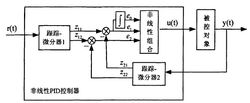参考输入信号，u(t)、y(t)分别是受控系统的输入和输出信号：非线性跟踪-微分器1、2的输出信号中 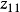、 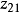分别跟踪 r(t) 和y(t)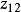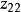， 、 分别为 r(t)和 y(t) 的微分信号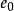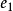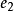； 、 、 是跟踪-微分器输出的参考输入和系统输出之间的偏差及其积分和微分变量1。

非线性PID控制模型非线性PID控制器可表示为：

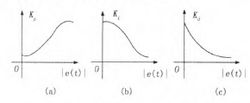
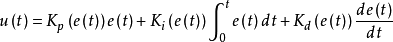
式中，Kp(e(t))、Ki(e(t))、Kd(e(t))分别为比例、积分和微分系数，它们都是误差的非线性函数。根据经典控制原理，系统阶跃响应过程中控制器P / I / D各部分的控制作用，相应的增益参数的理想变化如图2所示。

比例控制KpKp加快响应速度，减少过渡过程时间。为保证系统有足够的响应速度，Kp的大小应与误差的绝对值成正比，且当e(t)=0时，应保证Kp为合理的非零值，由此取比例系数的调节律为：

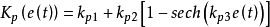
积分控制KiKi减少系统的稳态误差。当e(t)大时，Ki较大；当e(t)小时，Ki较小。所以积分系数的调节律为：

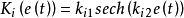
微分控制KdKd增大系统阻尼，降低过渡过程时间。在不影响速度的前提下，Kd应随e(t)逐渐增大，但同时应限制Kd以抑制超调。由此微分系数的调节律为：

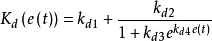
上述3式中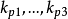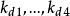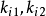，，，都为正实数。通过调整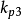、、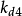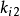的大小分别调整Kp、Kd、Ki的变化速率。按上述PID控制器参数在系统动态过程中的调节规律，即各参数与误差e(t)之间的非线性函数关系，分别调节控制器各部分的控制作用2。