[科普中国]-乘法电路

乘法器在当今数字信号处理以及其他诸多应用领域中起着十分重要的作用。随着科学技术的发展，许多研究人员已经开始试图设计一类拥有更高速率和低功耗，布局规律占用面积小，集成度高的乘法器。这样，就能让它们更加适用于高速率，低功耗的大规模集成电路的应用当中。

乘法器（multiplier）是一种完成两个互不相关的模拟信号相乘作用的电子器件。它可以将两个二进制数相乘。它是由更基本的加法器组成的。通常的乘法计算方法是添加和位移的算法。在并行乘法器当中，相加的部分乘积的数量是主要的参数。它决定了乘法器的性能。为了减少相加的部分乘积的数量，修正的Booth算法是最常用的一类算法。为了实现速度的提高Wallace树算法可以用来减少序列增加阶段的数量。我们进一步结合修正的booth算法和Wallace树算法，可以看到将它们集成到一块乘法器上的诸多优势。但是，随着并行化的增多，大量的部分乘积和中间求和的增加，会导致运行速度的下降。不规则的结构会增加硅板的面积，并且由于路由复杂而导致中间连接过程的增多继而导致功耗的增大。另一方面串并行乘法器牺牲了运行速度来获得更好的性能和功耗。因此，选择一款并行或串行乘法器实际上取决于它的应用性质1。

乘法代价很高并且运算很慢。许多计算问题的性能常常是由乘法运算所能执行的速度决定的。这一事实已促使设计者将整个乘法单元集成在例如现代数字信号处理器和微处理器中。

乘法器事实上就是一个复杂的加法器阵列考虑两个没有符号的二进制数X和Y甲分别为M位宽和N位宽。为犷说明乘法运算，可以用二进制形式来表示X和Y：

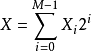
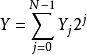
乘法运算定义如下：

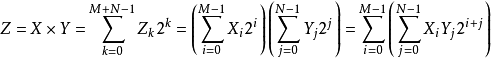
执行一个乘法运算最简单的是采用一个两输入的加法器。对于M和N位宽的输 ，乘法采用一个N位加法器时需要M个周期。这个乘法的移位和相加算法把M个部分积（partial product）加在一起。每一个部分积是通过将被乘数与乘数的一位相乘（这本质上是一个“与”操作），然后将结果移位到这个乘数位的位置得到的。

实现乘法的一个更快的办法是采用类似于手工计算乘法的方法。所有的部分积同时产生并组成一个阵列，运用多操作数相加来汁算最终的积。这一方法如图所示：

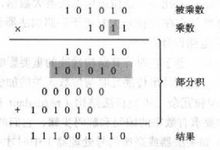
这一组操作可以直接映射到硬件；所形成的结构称为阵列乘法器（array multiplier），它结合了下面三个功能：产生部分积，累加部分积和最终相加2。

对于一个N比特的被乘数和一个N比特的乘数相乘的算法如下图所示：

一般来说

“与”门被用来产生部分乘积,如果被乘数是N比特，乘数是M比特，那么就会产生N*M个部分积，然而在不同结构和类型的乘法器当中，部分乘积的产生方式是不同的。 二进制的乘法可以被分解为加法。现考虑两个八比特的二进制数A和B相乘产生一个16比特的数。如下图：

满足这一方程：

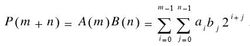
乘算法如下：

如果A的最低有效位是1，那么将B加到累加器中。

将A右移一比特，那么B左移了一比特。

当A的所有比特为0时停止。

从上面可以清晰地看出，数乘已经被转换成了加法运算。如果部分乘积被连续相加，因此一个串行加法器就可以和硬件一起使用。在组合电路中通过并行乘法器将所有的部分乘积相加是可以行的通的。然而，通过使用压缩技术，可以将部分乘积的数量降低。从这方面，是可以进行的。

一般结构的串/并行乘法器的结构如下图。将一个操作数并行送入电路中，而另一个数则串行输入。N个部分乘积组成每一个循环。在连续循环中，每一个循环结果作为M*N的乘法阵列的一列相加结果。最后的结果在2N个循环之后储存到输出寄存器当中。

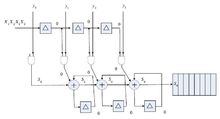
位移和添加乘法器的一般结构如下图所示，对于32比特的数乘运算，根据乘数最低有效位的数值，被乘数的数值被相加并累积。在每一个时钟循环周期内，乘数被左移一个比特，并且它的位值被测试，如果位值是0，则只进行一次位移操作。如果位值是1，则被加数被放入累加器中，并且左移一位。当所有乘数的比特值被测试完之后，结果就在累加器当中。累加器最初是N位，相加之后变成2N位，最低有效位包涵了乘数。延迟是N个最大循环周期。这类电路放在异步电路中有许多好处。

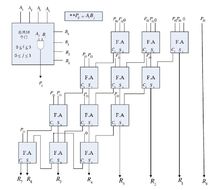
阵列乘法器因它规则的结构被大家熟知。乘法器电路是基于加法和位移的算法。每一个部分乘积是由被乘数和一个乘数比特相乘得到的。部分乘积根据它们的比特排列产生位移然后相加。整个相加过程可以在进位传输加法器当中完成。整个系统需要N-1个加法器并要求有乘数的长度。

这种计算方法是很简单的，加法在系统中是连续并行处理的。为了减小延迟和占用面积。逐位进位加法器可以用进位保留加法器取代。这样的话，每一个进位和求和信号都可以在下一个阶段通过加法器。最终的结果在最末端的加法器中获取。在阵列乘法器中我们需要相加的部分乘积要和乘数的比特数一样多。这种排列如下图所示：