[科普中国]-配电网扩展规划

简介

配电网规划问题是非常复杂的大规模组合优化问题。分支定界法是基于传统优化技术的配电网重构的优化方法之一 ，它是将重构问题表达成一个非线性或线性规划问题 ，然后用己相对成熟的规划优化方法进行求解 。

分支定界法与原始内点法相结合计算混合整数非线性规划 问题 目前在电力系统中主要应用于电网的无功优化计算在实际应用中，不但需要对新建区域进行规划 ，而且更常遇到的是在已有网架上进行扩展规划以满足负荷发展变化的需要。在目前的工程实践中，DG的容量和位置取决于发 电能源所处 的位置和能源储备情况 ，这已经由发电企业和城市管理部门进行确定 ，电力公司要根据DG规划调整配电网规划 ，以达到电网建设和运行费用最优。1

建模由于分布式电源的容量和位置已定 ，配电网扩展规划主要针对电网建设规划 ，建立配电网建设的固定投资费用 、配电网网损费用和运行维护费用综合最优的目标函数f。

目标函数的建立包括3个部分，第1部分为线路新建和变电站新建 、扩建的投资成本第2部分是电能损耗成本；第3部分是变 电站的运行维护成本。1

算法1、内点——分支定界法

内点——分支定界法是现代 内点算法和分支定界法结合而成的混合算法 ，能够精确求解离散变量和连续变量同时存在的0 ～1混合整数规划问题。分支定界法能把离散变量的整数规划转化为仅含连续变量的规划问题 ，而内点算法能求解仅含连续变量的规划问题。

随着分支的进行 ，原问题的子问题越来越庞大。为了加快计算速度 ，减少计算量 ，算法对所有子问题进行剪支判断 ，对满足剪支准则的子问题进行剪支 ，不满足准则的子问题进行分支 ，一直到所有分支子问题已经全 部处理完毕 得到问题的最优解。

2、算法流程

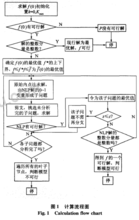
基于投资最小配电网扩展规划的数学模型 ，采用内点——分支定界法求解，下面归纳其算法流程 ，图 1 为计算流程图。

在图1剪支中，满足以下3个条件可对分支节点进行剪支 ，及时删除不可行的分支 ，减少工作量加快计算速度 ，避免问题收敛于局部最优解。

(1)如果该分支不满足安全约束 ，则该分支问题不可行 ；

(2 )如果所求的目标值最优解ffound满足ffound>f*+ε；

(3 )若所求最优解小于f*，则 f*=ffound将其转向条件 b。

如果分支层不满足于上述 3 种情况 ，求解下一个候选分支 ，如果满足则对于不可行子 问题 ，从待分支列队和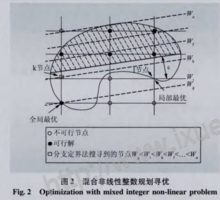已经取得子问题队列中删除；对已经得到整数解的松弛子问题从待分支队列中删除，此时已经取得子问题存储整数可行解信息，另外对于为满足整数解要求的松弛子问题加入到待分支队列中。

利用分支定界法求解混合数线性规划时，子一代分支层的目标函数总是大于或等于父代分支层的目标函数。但在混合非线性规划整数规划中，子一代分支层的目标函数不一定总是大于或等于父代分支层的目标函数。为此在条件b中引入了一个安全因子ε，其作用如图2所示。若无ε则nodel节点为最优点，求解陷入局部最优，安全因子ε保证在global点找到全局最优解。1

与电网规划的关系电网规划又称输电系统规划，以负荷预测和电源规划为基础。电网规划确定在何时、何地投建何种类型的输电线路及其回路数，以达到规划周期内所需要的输电能力，在满足各项技术指标的前提下使输电系统的费用最小。

电网规划按照时间分类，可以分为短期规划、中期规划和长期规划。

另外还可以按照不同专业进行分类，比如通信规划、营销规划和煤矿电源规划等各种专项规划。

短期规划分为1-5年，规划的内容比较具体仔细，可直接用来指导建设。一般的电网5年规划与国民经济5年规划的时间同步。如，十一五规划、十二五规划等。

中期规划一般为5－10年。

长期规划则需要考虑比输变电工程建设周期更长的发展情况，一般规划6-30年。长期电网规划需要列举各种可能的过度反感、估计各种不确定因素的影响等。长期规划的方案并不一定在建设中原封不动的实施。由于客观条件或环境的改变，规划方案也将不断变化。

电网规划理论计算上已成功运用遗传算法、模拟退火等多参数并行算法进行线路规划，并应用于实际，取得了良好效果，保证了规划方案的最优选择，这将是城网规划的趋势。

城网规划工作在服务与服从市政规划工作的同时，供电企业也要根据自己的财务状况拿出自己的规划标准，及时与市政规划部门沟通，避免由于市政规划部门过分注重科学技术的提高，在市政规划中对供电企业提出过高的技术标准，使供电企业承受较高的投资。

对于一个拥有巨大固定资产额的供电企业而言，要想保证良好的资产负债率与利润率，必须争取城市电网多元化投资的实现。这既影响到了供电企业当年的经营业绩，更影响到了供电企业的可持续发展问题。

总结1、以目标函数为配电网建设的投资费用 (包括新建和改扩建变电站和新建线路) 、配电网网损费用和运行维护费用综合最优的非线性整数规划模型 ，并以严格的数学模型保证配电网辐射结构运行方式。1

2、采用内点——分支定界法进行求解。基于广度优先遍历的分支定界法结合原始对偶内点法对大规模的配电网系统进行扩展规划，通过分支节点的剪支，加快计算速度 ，实现了精确求解混合整数规划的全局最优解 。通过算例进行仿真计算 ，得到合理的最优解。但随着系统规模 的增大 ，离散变量的增加使得分支的次数显著增多 ，分支定界法求解子问题的数目急剧增加 ，求解非常耗时 ，这也是分支定界法的一个缺点。基于现代飞速发展的计算机技术，为了解决求解大规模配电网网络重构最优的单机运算耗时巨大的矛盾 ，以达到最佳的优化效果 ，可 以考虑采用并行或是分布式的计算方法 以实现快速和高效地求解全局最优解。2