[科普中国]-自适应网格技术

简介

自适应网格技术是针对包含多尺度结构流场进行数值模拟提出的，能从根本上去除套网格所带来的弊端。它是通过坐标变换，把物理域上不规整网格变换到计算域上规整的网格，使得网格的移动写进控制方程中，并在每一步的求解中得以实现。

自适应网格技术首先从航空航天领域发展起来的，80年代在计算流体力学领域已有较广泛的应用。Dietachmayer和Droegemeier在1992年称他们第一次将这一技术应用到气象学领域，实际上我国学者刘卓在1991年曾对这一技术在气象学上应用有过专门的研究。自适应网格技术分为两类:一类是网格点数固定，通过移动网格在解的大梯度区自动加密网格;另一类是网格点数可以变化，此法多用于有限元方法中。第一类方法是由Brackbill和Saltzman所提出，其要点是:根据各网格间解的梯度值取一个权函数w，并使得w*△x=常数。这样，某网格间上解的梯度值越大，权函数就越大，相应的△x就越小。为达到这一目的，先将其转化为一个变分问题，通过求解其欧拉方程来得到新网格点位置。1

定义自适应网格技术是指在数值计算过程中，可以根据解的变化和需要，计算网格能自动进行调整，以提高数值计算效率和精度的技术。

网格描述自适应网格是由一系列重叠网格序列嵌套而成，计算刚开始时，由用户给定粗网格，定义为基网格，记作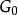，在整个计算过程中保持不变，如果初始计算区域是分片的，那么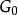可能有几个网格了片构成，嵌套在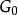中的细网格，称为网格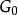的了网格，称为1级细化网格，记为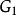，可能包含多个网格，记作, l=1,2...，同理嵌套在以中的细网格，称为网格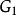的子网格，记作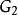，称为2级细化网格，依次类推。在所有的细化级中采用相同的加密比率，时问步长按照相同加密比率处理。总之，这样最终可以形成一种动态多层嵌套网格系统。

这里要引入几个概念：

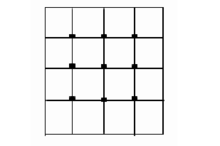
网格效率：加密的网格点数与总网格点数的比率。图所示，加密的点用黑点表示，网格效率为9/25 = 0.36。加密比率取值一般要在0.6以上，加密比率越高，数值模拟的结果越好，但是时间开销越大。

缓冲区:由于守恒律方程解的问断随时问推移而移动，因此在细网格生成以后，需要在细网格周围添加几个网格，以免在下次重新生成网格之前，问断脱离加密区域。典型的缓冲区大小2或4个网格。

重新生成网格的频率:每隔多少个粗网格时间步重新进行误差估计，生成新的网格结构。典型的频率是3一4个粗网格时间步。2

权函数权函数的选取决定了分配网格的法则，不同问题因其流场结构不同，所选用的权函数也不同。选一个好的权函数能有效地提高自适应网格的效率.对运动激波算例，由于激波两端更容易产生振荡，因此权函数考虑二阶导数项比考虑梯度项更能有效地减小误差，提高精度;对气旋锋生算例，仅考虑梯度的权函数并不能提高精度，必须考虑速度场和锋生函数分布等的权函数才能更合理地安排网格，提高精度。

应用自适应网格技术对冲压成型是至关重要的，因为初始的冲压板材通常比较平坦、形状很简单，采用有限元网格离散化时，如果网格较粗，可能引起较大误差。但如果采用细密的有限元网格，将增加单元的总数，并且由于单元尺寸减小将降低极限时步长，增加计算的机时。虽然采用局部细分网格可以节省机时，但由于板料大变形和在模具中相对滑动，难以预测局部细分网格在初始状态板料上的位置，而且局部细分网格在前处理时也有很大麻烦。自适应网格技术刚好解决了这一问题，并在时间与精度上巧妙地取得了平衡。自适应网格技术提高了对零件的表面质量(表面缺陷、擦伤、微皱纹等现象)判断的准确性，并且可以节约大量的计算时间。3

优点（1）自适应网格技术能有效地减少大梯度区的网格间距，因而能减小误差，提高精度；

（2）自适应网格技术能显著地降低运行时间，并节省内存；

（3）自适应网格技术使得梯度不大的区域网格间距大，因而能更快地传递边值信息，使收敛加快；

（4）自适应网格技术不论对线性的对流扩散问题、还是对非线性的Burgers方程，不论对定常问题、还是对非定常问题，不论对有大梯度解的情况、还是对没有大梯度解的情况，其计算结果均显示出了其优良的性能。