[科普中国]-隐藏线消除-

概况

隐藏线及隐藏面消除问题自六十年代中期以来一直是计算机图示领域中一个十分活跃的分支。问题的提出在于随着计算机图示的应用日益广泛，实用上对图象的逼真性及立体感要求愈来愈高。早期所用的显示设备限于划线式显示器，隐藏线消除技术成为竞相研究的重点。后来光栅扫描显示器日益普及，注意力又转向隐藏面消除技术的研究。由于光栅扫描显示设备分辨率的限制及离散效应的影响，不能显示图象精细细节,加之扫描转换速度不适应对话式显示的要求，所以在高质量工程图及对话式显示方面线型图具有独特的优点,仍需深人研究。

基本步骤隐藏线消除的基本步骤：

1.数据准备

为适应消去隐藏线的操作，连续的三维物体首先需要平面化。多面体自然由平面构成，曲而体可用一定数量的小平面来近似表示。这些平面及小平面统一用多边形来表示(一般以四边形为方便、多边形可分解为四边形)。经过这样简化，三维物体的几何信息一般只需储存各四边形顶点的座标值以及顶点的连接关系。

座标信息按照应用场合进一步施以透视变换或平行投影变换。

2.数据整理

将数据进行分组与排序，以便于检索及避免一些不必要的运算或操作。

3.初步判别

凡用简捷方法就能判明可见性的部分不要放在下一步去做，如消去背影面往往可去除一半左右的基本元素，大大减少下一步判别的工作量。

4.比较判别

判定基本元素如格子点或格子线(四边形的顶点及边)是否可见或哪一部分可见。

5.连线成图

按一定逻辑将可见点或线段连结起来。

运算及操作分类及检索消除隐藏线的算法往往要处理大量数据，而且算法执行的各种操作又常在某些特定数据上进行。因而用恰当的方法(具体方法可参看有关专著)将数据按某种特征分类排序，并采用快捷的检素方法检出所需处理的数据，这是提高整个算法的频率的关键措施之一。

最大最小方框判别对投影平面xy面上的一线段或一多边形，通过其中具有xmax及xmin值的顶点(端点)且平行于Y轴的两直线段与通过具有ymax及ymin。值的顶点(端点)且平行于X轴的两线段围成的矩形称为最大最小方框。
若两方框不相交，则可粗略地认为对应框内之多边形或线段相互间不影响可见性。实现这种判别操作仅需简捷几步，适合于初步判别阶段快速剔除大量可见性无关之元素，或在判别阶段中用以迅速挑选比较对象。

包围检验
判别一点是否被一多边形包围或被一多面体包围是可见性判别时常用的操作。
利用平面方程可以判别一个点是否被多面体包围。将该点座标值代入平面方程(一般式)，若方程右端不等于零，则表示该点位于平面一侧。适当选择方程系数的符号，可以判定一个点在多，面体内部还是在外部，若是前者则被包围。

算法隐藏线消除问题的算法尽管繁多，但每一算法都是为解决某一特定类型的问题而设计的。按照所处理的对象的几何特性，现有算法可分类如下：
1.多面体型 2.曲面体型 3.复合体型

多面体型算法这类算法处理由多面体构成的图象。现有文献中属于此类问题者占有较大比重。最早提出多面体型隐藏线消除算法系L. G. Roberts，而Griffiths的算法是其中较简易、不受图象复杂程度限制而且可得到精细画面的一个。

Griffiths的算法把多面体的棱边作为基本元素，将其与多面体的每个面相比较，以判别棱边上哪些部分被遮住而看不见，即所谓“边一一面’比较法。

他采用右手坐标系。Y轴正向朝上，X轴正向指向观察者右侧。连结两点(x1, y1, z1)与(x2,y2,z2)的直线段用下列方程表示

x=x1+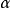(x2-x1)

y=y1+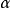(y2-y1)

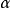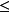
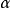
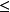z=z1+(z2-z1)

一条被检验的棱边与视点(投影中心)构成一三角形，这个三角形与多面体中一个面(通常以多边形表示)相交，其交线称之为屏障线。利用屏障线可判定一棱边的可见性。图中屏障线GN能影响被检边AF哪一段HM称为有效段。求解AF与E形多边形各边的联立方程可得屏障线与该多边形的交点，因为HM与AF在X一Y面具有相同的透视投影。屏障线GN被分割成数段HI,IJ等，其分点亦用α来标识。利用各交点与多边形顶点之关系可求出屏障线上各分点处的深度值，即Z坐标值。记被检边中点处深度值为Ze，屏障线中点处为Zm，若Zm