[科普中国]-轨迹线性化控制

基本概念

轨迹线性化控制(Trajectory Linearization Control，TLC) 方法是一种基于微分代数谱理论的非线性控制方法，在NASA先进制导控制项目中被成功应用于X-33的上升段姿控系统设计。

TLC方法的设计思想在多数控制问题中，设计控制器的目的是希望被控对象的状态或输出在控制律的作用下跟踪期望的标称指令，在飞控问题中就是要求飞行器的姿态能够快速准确地跟踪制导系统发出的姿态角命令。TLC方法的设计思想是：首先利用非线性动态逆方法将轨迹跟踪问题转化为一个跟踪误差调节问题，然后利用线性时变系统PD谱理论设计状态反馈控制律, 使得该误差跟踪系统一致渐近稳定。控制器结构如图1所示1。

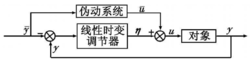图1

考虑如下形式的多输入多输出非线性系统：

定义如下的状态跟踪误差：

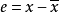
并构造控制律为：

其中，η即为所需设计的线性时变反馈控制律。则对应的非线性跟踪误差动态系统为：

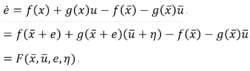
此时，原非线性系统跟踪问题就转化为一个非线性调节问题，控制器包括两部分：

（1）一个开环的被控对象的伪动态逆控制器, 根据期望的系统输出值 y产生一个标称的控制输入 u;

（2）一个闭环的线性时变反馈调节器η=η(e)用以镇定系统, 并使系统具有一定的响应特性。

结构TLC（其概念如图2所示）结构由两部分组成：通过非线性模型伪逆求得给定标称输出η(t)对应的标称控制量μ(t) ，以粗略对消系统的非线性，并将一般的轨迹跟踪问题转化为在误差坐标系的状态调节问题，上方带“－”的变量为变量的标称值; 将非线性时变误差动力学方程组线性化，通过李雅普诺夫坐标变换将一般的线性时变方程组转化为线性时变系统标准型，并通过配置Parallel Differential Spectrum(PD谱)对误差动态进行镇定。反馈控制项μ(t)由时变镇定控制器产生，并可写为状态误差量的线性反馈形式μ(t)=K(t)ξ(t)。

TLC 对跟踪误差信号可以保证指数稳定性，闭环系统对正则扰动及奇异摄动都有很好的适应性。

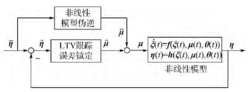图2

LQR与TLC在制导中的应用比较线性二次型调节器( Linear Quadratic Regulator，LQR) 控制由于反馈增益可以采用误差状态的线性反馈控制律构成最优闭环，设计时能够考虑允许的状态偏差和控制量偏差等多个指标，在参数不确定的情况下闭环系统也具有一定鲁棒性，在多入多出系统的控制方面获得了较多应用。

与LQR方法相比，TLC方法具有更宽的适应范围，其原因在于基于LQR的增益调度方法需要求解Riccati方程，通常难以实时求得最优反馈增益，一般只能根据设计好的参考轨迹离线计算获得后存储于制导计算机。为了适应不同的参考轨迹，只能在地面离线生成多组增益，应用时需要根据实际采用的参考轨迹来选用对应的制导反馈增益。由于设计中通常无法考虑所有的非理想情形，因此采用这类制导律设计具有潜在的风险。而TLC方法不依赖于参考轨迹，反馈增益可以符号化表示为参考轨迹的函数，并只需计算简单的代和增益大小与无量纲自然频率直接相关；对于参考轨迹的不同阶段或差别较大的参考轨迹，通过在线改变不同环路自然频率的数值（同时保证环路间带宽的分离）即可实现期望的控制效果；另外，TLC方法需要调整的参数数量很少且调整的方向性非常明确。这些区别使得TLC方法不仅可以适应更宽范围的再入飞行制导任务，而且与轨迹在线生成算法一起将可极大提高再入制导的自主性，适应于应急再入任务规划、在线任务改变或落点调整等情形。

（1）TLC方法在初始状态拉偏和扰动情况下也能实现很高的跟踪精度，体现了方法的有效性和鲁棒性。

（2）与LQR方法的仿真结果相比，TLC需要调整的参数更少，参数的选取更直观，对不同参考轨迹有很好的适应性，是一种完全在线的非线性控制方法。与近似滚动时域控制相比，TLC在控制精度略优于前者的情况下计算量显著减小。

（3）在再入轨迹跟踪制导律中使用TLC控制，可以做到制导环和姿态环控制结构的统一和设计时的一体化；高度、速度、姿态角和姿态角速度的四环路TLC控制策略将更便于制导和控制参数的匹配和实时调整。

因此，TLC跟踪制导策略对于减少制导指令的解算时间，提高制导的自主性、适应性和精度有一定工程意义2。