[科普中国]-边界表示

将一幅图像分割成不同区域后，使用更适合于计算机进一步处理的形式，对得到的被分割的像素集进行表示和描述。因此，图像表示与描述是图像识别和理解中的重要工作。

图像的表示包括两种：基于外部特性的边界表示和基于内部特性的区域表示。图像的表示完成了将数据转换成可用于计算机处理的形式的目的。

边界表示关注的是图像中区域的形状特征，常用的方法有链码、边界分段、多边形近似、标记图等；区域表示关注的是图像中区域的的灰度、颜色、纹理等特征，常用的方法有四叉树、骨架等。

图像的表示完成后，要选择适当的图像描述方式。一般，图像的描述采用二维描述，它也分边界描述和区域描述两大类。常用的描述方法有边界描述、区域描述和形态学描述。1

链码链码用于表示由顺次连接的具有指定长度和方向的直线段组成的边界线。典型的表示方法是根据链的斜率不同，有4链码或8链码。每一段的方向是用数字编号方法进行编码。

4链码：在链码的四个方向上移动，以数字集合{i|i=0,1,2,3}编码来表示与x轴的夹角为90°× i。

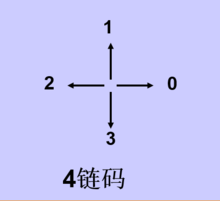
类似地，6链码的相邻方向之间的夹角为60°，8链码的相邻方向之间的夹角为45°。

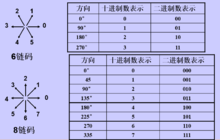
表示方法：

在目标边界上任意选取某个起始点，从该点坐标开始，将水平方向坐标和垂直方向坐标分成等间隔的网格，然后对每个网格中的线段用一个接近的方向码来表示，最后，按照逆时针（或顺时针）方向沿着边界将这些方向码连接起来，即得到链码。

存在的问题：

1）得到的链码有时太长；

2）噪声或边界线段的缺陷都会在边界上产生干扰。

解决办法：

选择更大间隔的网格对边界进行重新取样，达到减少边界点、降低噪声干扰的敏感度的目的。

起始点的选择：

边界的链码依赖起始点。由于链码的起始点任意选择，对同一边界如果选用不同的起始点，常常会得到不同的链码。

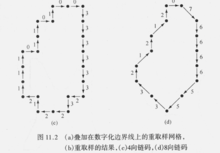
起始点归一化：

将链码看作一个循环序列，依次取各个边界作为起始点，从得到的所有链码中选取构成自然数值最小的码作为归一化结果，该最小码值的点即为归一化后的起始点。

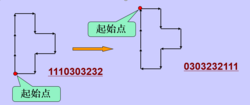
链码旋转归一化：

链码具有平移不变性，即当边界平移时，其链码不发生改变。但是，当边界旋转时，则链码会改变。

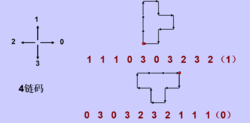
旋转归一化方法：

用链码的一阶差分码作为新的码。一阶差分即为相邻两个方向之间的变化值。

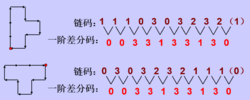
可见，当原边界旋转为新边界时，其码链改变，但它们的一阶差分码不改变。1

边界分段边界分段是将边界分成若干段，分别对每一段进行表示。特点是降低边界复杂程度，简化表示过程特别适用于边界具有多个凹点的情况。

方法：构造包含边界最小凸集的凸包，跟踪区域凸包的边界，记录凸包边界进出区域的转变点，实现对边界的分割。

多边形近似多边形的边可用线性关系表示。对一条闭合曲线，当多边形的边数等于边界上的点数时，这种近似是准确的，此时，每对相邻点定义多边形的一条边。

最小周长多边形法

以周长最小的多边形来近似表示边界，即将边界看成是介于多边形内外界限之间有弹性的线，当它在内外界限的限制之下收缩紧绷的时候，即可得到最小周长边界。

算法实现：

假设用一系列彼此连接的小单元将一条边界包住，这条由单元组成的环带使包围圈像一条有弹性的线，当它收紧时即可得到最小周长边界。

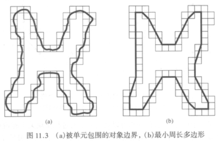
多边形近似问题常用聚合技术和拆分技术来实现。

聚合技术：

基于平均误差或其它准则的技术。

例如沿边界线寻找聚合点，直到适合聚合点的最小平方误差线超过一个预先设置的门限，这时就将点聚合，即获得一条直线。然后继续沿着边界线寻找，直到误差再次超过门限聚合新的点。这个过程不断重复，最后线段的交点构成多边形的顶点。

存在的问题：

得到的近似图形的顶点不总是与原来边界的拐点一致，因为新的线段只有超过误差门限才开始。

拆分技术：

将一条线段不断地分割为两部分，直到满足定好的某一标准。

例如，某标准定为：从边界线到某一直线的的最大垂直距离不超过预定门限，而这条直线要求连接此边界线的两个端点。如果这个条件满足，则距离此直线的最远点成为一个顶点，这样，将初始的线段再分为两条子线段。1

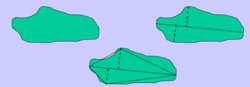
标记图标记图是一种用一维函数表达二维边界的方法，以达到降低表达难度的目的。它可以用多种方法生成。最简单的方法是把从重心到边界的距离作为角度的函数来标记。

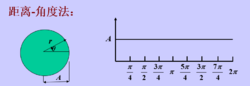
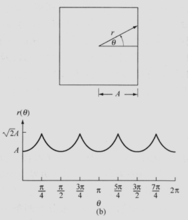
特点:

该方法不受边界平移的影响,但是当边界旋转或发生尺度变换时，标记将会发生改变。可以用归一化方法进行解决。