[科普中国]-数字微分器

基本概念

微分运算是一种基本的数学运算，在信号分析与处理等领域得到广泛应用，特别在信号的奇异性检测和提取方面具有特殊的作用。我们常用的微分运算，微分方程等使用的都是整数阶，例如一阶导数、二阶导数⋯，一阶微分方程、二阶微分方程⋯，然而许多事物、自然现象以及社会现象，例如诸多“非”问题和现象是难以用整数阶微分方程来描述和刻画的。从信号分析与处理角度来看，微分运算，即对函数或信号f(t)求导：

数字微分器，是指执行微分运算的数字方式。整数阶数字微分器用于确定和估计给定信号的（一般是关于时间）导数是十分有用的工具。例如，在雷达和声纳应用中，速度和加速度是用微分器从位置测量数据计算出来的。在生物医学工程中，通常需要获得生物医学数据中，特别是在低频区间的高阶导数。对于整数阶，也即普通微分滤波器的设计理论己很成熟并得到广泛应用。

理想数字微分器设计定义从信号处理角度来看，整数阶或分数阶（阶数为v）微积分运算完全可以看成是对信号的滤波，滤波函数即是1

有如下三种情况：

（1）v>0，对应于微分函数

是奇异高通滤波；

（2）v=0，对应于全通函数

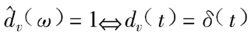
（3）v