[科普中国]-非线性模型预测控制

预测控制算法最初是对线性系统提出的。当对象存在弱非线性时，采用这种线性预测控制算法也是十分有效的，因为弱非线性可视为一种模型失配，其影响可通过系统的鲁棒性设计加以克服；必要时，还可通过在线辨识和自校正策略修改模型和控制律，以适应因弱非线性而引起对象特征的变化。但是几乎所有的实际控制系统都是非线性的，尤其是在实际的工业生产过程中，涉及的对象往往都是多输入多输出的复杂系统，具有很强的非线性，由于采用线性模型进行预测输出与实际偏离较大，达不到优化控制的目的，模型线性化这一方法显然不适用，因而必须基于非线性模型进行预测和优化。因此，提出了非线性模型预测控制方法。12

各类模型预测控制(MPC)算法虽然在模型、控制和性能上存在许多差异， 但其核心都是在每个采样周期，以系统当前状态为起点，在线求解有限时域开环最优问题，得到一个最优控制序列，并将该序列的第一个控制量作用于被控系统，作为一种有限时域滚动优化策略，MPC 具有三个基本要素：预测模型、滚动优化和反馈校正。这一算法的基本结构如图 1 所示，其基本原理图如 2 所示。

图中，y 是系统当前输出， 是根据设定值 w 和 y 求得的参考轨迹，

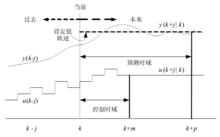
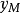
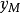是预测模型的直接输出， 是经反馈校正后的预测输出，虚线部分 将与 y 之间的偏差 e 反馈给预测器以便进行反馈校正。各部分的功能如下：

参考轨迹：它对改善闭环系统的动态特性及鲁棒性起重要作用，根据 y 和设定值生成的 是从系统当前输出到设定值的一条光滑轨迹。

滚动优化：在每个采样周期，求解有限时域优化问题，并将求出的最优控制序列中对应当前时刻的部分应用于被控对象。

预测模型和预测器：基于模型和系统信息求出预测值 ,并根据过去的预测偏差信息，对其进行反馈校正，得到校正后的预测输出 。1

在非线性模型预测控制中，系统模型是非线性的，因此，相应的预测模型也是非线性的，设非线性系统的模型：

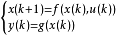
其中， ， ， 。根据这一模型，在 k 时刻只要知道对象的初始状态x(k)及其未来的控制输入 u(k),u(k+1),…，便可预测对象在未来各时刻的模型输出 。

其中，i=1,2,...。

通过递推，可以得到非线性系统的预测模型： 其中，是由 f(·)及 g(·)复合而成的非线性函数。

由于实际受控系统总包含某些不确定因素，利用上述模型预测，不能完全精确地描述对象的动态行为，因此可以在实测输出的基础上通过误差预测和补偿对预测模型进行反馈校正。记 k 时刻测得的实际输出为 y(k)，则可由 构成预测误差，并根据历史的误差信息 e(k),…,e(k-q)，通过误差预测 校正基于模型的预测，并构成对输出的闭环预测。其中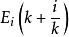， 为某一线性或非线性函数，其形式取决于所用的非因果预测方法，在 k 时刻，控制的目的是要求算出该时刻起的 M 个控制量 u(k), …u(k+M-1)(假设 u 在k+M-1 时刻后保持不变)，使输出某一性能指标最优：

其中，

式中， w( k + i)为 k+i 时刻的期望输出，M，P 的含义与线性预测控制相同。这样，在线的滚动优化就是在闭环预测（下式）的约束下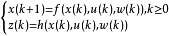，寻找控制作用使性能指标取极小的问题。如果可由此求出最优的u *( k ),...,u *( k + M− 1)，则在 k 时刻实施控制 u *( k )。到下一个采样时刻，检测系统的实际输出进行误差校正后，又重复进行优化，这就是非线性系统预测控制问题的一般描述。1

线性化方法是研究非线性系统的常规方法。将非线性系统局部线性化主要是为了沿用线性系统中已有的成果，计算简单，实时性好。对于非线性较强的系统，用单个线性化模型很难反映系统在大范围内的动、静态特性，控制品质甚至稳定性都难以保证。因此实际处理时，有以下三种线性化方法。

（1）将非线性机理模型在每个采样点附近线性化，然后对线性化的模型采用线性的预测控制算法，其特点是在每个采样时刻都采用新的模型，能尽量减小线性化带来的误差。但是频繁的在线更换模型会导致需要反复计算相关矩阵参数，计算量加大，且不利于离线对控制器的参数进行优化设计。

（2）多模型方法。顾名思义，就是引入区间近似的思想，用多个线性化的模型来描述同一个非线性的对象。多模型方法的优点在于可以离线的计算大部分控制参数，难点则是如何确定模型切换的时机以及保证模型切换时的平稳性。

（3）反馈线性化（即就是 I/O 扩展线性化）的方法，即对非线性系统引入非线性反馈补偿律，使非线性系统对虚拟控制输入量实现线性化，便可以使用线性的 MPC方法。也有许多非线性系统不满足反馈线性化的条件，使其应用受到限制。

常用的非线性模型包括 volterra 模型、Hammerstein 模型、Wiener 模型等。volterra模型为非线性对象的广义脉冲响应模型，可以描述一类非线性对象的输入输出特性，实际应用中常采用正、负和双阶跃响应法建立系统的 volterra 模型。Hammerstein 模型和 Wiener 模型都是由一个非线性的静态子系统和一个线性的动态子系统串联而成，二者的区别是串联的顺序不同。

神经网络以其分布式存储、并行处理、良好的鲁棒性、自适应性、自学习性，在控制界具有广阔的应用前景。由于神经网络能够以良好的精度逼近非线性函数，且基于神经网络的建模方法具有普遍性，因此在非线性预测控制中受到重视，相关的研究成果也比较多。

关于采用神经网络的预测控制，存在的困难也比较多，主要是还不能有效地进行多步预测，而通常来说多步预测的控制效果要明显优于单步预测。尽管将多个神经网络串联可以得到多步的输出预测，但这样会增加控制器的复杂程度，直接影响控制量的求解。同时，如果需要在线进行模型辨识，那么在线的网络训练需要较长的时间，控制的实时性变差。1

（1）非线性建模。建立一个用于非线性预测的高质量对象模型是提高预测控制性能的前提条件，由于控制器的设计是在模型先验知识的基础上进行，而控制器的性能也会受到建模误差的影响。工业生产中对象的不确定性和大规模特性，使得非线性建模，特别是建立具有多步预测功能的模型，具有非常大的挑战性和现实意义。

（2）滚动优化算法研究。线性的预测控制方法之所以能够在工业上取得成功的应用，部分原因是这类问题的滚动优化都有有效的求解方法。非线性预测控制器每次采样时刻都要求解一个非线性规划，计算量大，而且缺乏有效的工具。研究一种适用性广且效率高的优化算法，是一个具有挑战性的课题。

（3）稳定性分析。在优化问题中加入稳定性约束（如终端约束或不等式约束、收缩约束），似乎从理论上解决了 MPC 的稳定性问题，但从工程应用意义上说，还没有一种完全令人满意的方法。首先，稳定性约束是人为附加的，可能会影响控制性能指标的实现；其次，稳定性约束将引起优化问题的可行性问题。

（4）过程应用。大多数非线性预测控制算法的应用还局限于各种仿真过程，现在迫切需要将理论研究成果推广到实际过程应用中，能真正解决一些问题，并从中发现新问题，从而推动理论和实践的前进。1