[科普中国]-小脑模型关节控制器网络

小脑模型关节控制器（CMAC）是由含局部调整，相互覆盖接受域的神经元组成，J.S.Albus于20世纪70年代提出了CMAC，它是模拟人的小脑的一种学习结构，是基于表格查询式输入输出的局部神经网络模型，提供了一种从输入到输出的多维非线性映射能力。由于CMAC具有学习速度快、泛化能力强、易于实现、不存在局部极小点等特点，被广泛地应用于对实现性要求较高的控制系统中，作为辩识器和控制器，并取得了较好的效果。

其结构见图1所示，由两个基本映射表示输入输出之间的非线性关系。

图1

（1）概念映射（X→ AC）

设n维输入向量为X，经量化编码后，映射至AC中c个存储单元中，在输入空间邻近的两个点，AC中有部分的重叠单元被激励。距离越近，重叠越多；距离远的点，AC中不重叠，即相近的输入产生相近的输出。

（2）实际映射（AC→AP）

实际映射是由概念存储器AC的c个单元映射至实际存储器AP的c个单元，这c个单元中存放着相应的权值，则网络的输出为AP中c个单元的权值之和。

在CMAC中，若输入维数较高，则AC要有很大的容量。但对于特定的问题，在AC中被激励的非零单元是很稀疏的，用杂散存储，可将AC空间压缩到较小的AP中。

传统的CMAC网络权值的调整一般采用Widrow-Hoff规则，即LMS方法，如下式1：

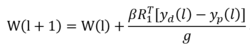
其中，g是泛化常数， 是学习率。

这种算法实现容易、学习速度快，但它是用分段超平面去拟和非线性超曲面，因此，不能学习所逼近的导数，并且精度不高。很多学者对CMAC的学习算法进行改进，进而达到提高网络收敛速度和精度的目的。其中最具代表性的是Chang-TsanChinang和Hun-ShinLin于1996年提出在输出层引入了广义基函数（GBF）取代了原有网络输出层上的线形映射。可以说是CMAC研究的一大突破。它的优越之处在于当基函数采用可微函数时，可记忆系统的微分信息，而传统的CMAC可看作是基函数为1的网络。当然，其代价是增大了计算量，并且收敛速度比传统CMAC网络大大降低。其连接权的学习算法为：

其输出为：

其中： 为基函数，可用B样条插值函数等。

为了克服广义基函数CMAC的缺陷，很多学者在此基础上又做了进一步的改进，如段培勇等在此基础上提出了改进的基于广义基函数的CMAC学习算法，使收敛条件不依赖于基函数和样本数据，且学习速度快。

从某种意义上来说，CMAC与模糊逻辑不但是相互补充的，而且也是相通的、可以结合的。首先，利用连接主义表达的模糊逻辑控制器必然要引入学习机制，也带来了两者结合的诸多优点，如存储容量的减小，泛化能力的提高以及连接主义结构的容错性等。其次，CMAC的分布表达式中，一个值由散布于许多计算单元的活性模式表示，每个计算单元有涉及许多不同值的表达，因此每个计算单元都有一个感受野，即它所表达的所有值的集合，这相当于每个计算单元都对应一个模糊集合，或者说感受野相当于隶属函数。这正是它们能够相结合的一个基础。因此，基于模糊的CMAC也不断地被广大学者所关注，有着很好的应用前景。

1992年，Wong对CMAC的收敛性进行了分析，得出了当采用增量学习法，学习率为1时，CMAC算法CMAC算法本身保证了它的收敛性的结论，当输入是多维时，上述结论不一定成立。其他人在Wong的基础上，对CMAC的收敛性进行了进一步研究但其结论是在关联矩阵正定的特殊条件下得到的。何超等在Wong提出的算法表达形式出发，分析了CMAC增量算法在批量和增量两种学习方式下的收敛性，给出这种算法的一般性定理：

定理1

CMAC批量学习算法的充要条件是学习率满足

其中，λmax>0是关联矩阵C的最大特征值。

定理2

CMAC增量学习算法的必要条件是学习率满足0