[科普中国]-尼奎斯特曲线

简化Nyquist稳定判据的描述

由于对于一个稳定的闭环系统来说，其在S右半平面肯定是无特征根，即Z=0，因此，Nyquist稳定判据就可以这样认为，若Nyquist曲线包圈(-1，j0)点的圈数等于开环传函在S右半平面的极点数，则闭环系统稳定。进而，若开环传函在S右半平面无极点，即P0，则闭环就稳定的充分必要条件是Nyquist曲线不包围(-1，j0)点。

Nyquist曲线的简介对于w的复变函数G(jw)有：

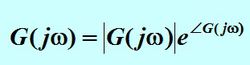
当ω从0→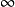 变化时，矢量G(jw)的端点在复平面上形成的轨迹叫作G(jω)的极坐标图或Nyquist图，该轨迹就是Nyquist曲线。

Nyquist图的优点是：在概念分析上比较清楚、直观，特别在分析系统稳定性上经常用到。Nyquist图的缺点点是：极坐标图画起来复杂，运算也较繁琐，要遵循矢量运算规则。

Nyquist曲线绘制步骤Nyquist曲线绘制的大致步骤如下：

（1）写出系统开环传递函数的频率特性；

（2）确定开环幅相曲线的起点 ；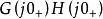

（3）确定开环幅相曲线的终点 ；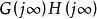

（4）确定开环幅相曲线与实轴是否有交点，若有，则该点的频率特性虚部为零；

（5）确定开环幅相曲线与虚轴是否有交点，若有，则该点的频率特性实部为零；

（6）勾画出开环幅相曲线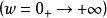 的大致曲线(越精确越好)。

Nyquist曲线绘制的注意事项(1) 若系统开环传递函数中出现积分环节，说明系统中有零极点，则应对Nyguist曲线进行修正后，才能使用Nyguist稳定判据进行判断。若开环传递函数中有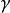个积分环节，则先绘出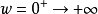的Nyguist曲线，然后从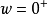开始，逆时针方向补画一个半径为无穷大，相角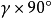为的大圆弧，即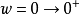补画的曲线，然后再根据Nyguist稳定判据判断闭环系统的稳定性。

(2) G(jw)与G(-jw)关于实轴对称，因此只需要w从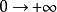的Nyguist曲线即可。

(3) 若存在多个环节，应注意随着w的增加、角度的变化过程以决定Nyguist曲线的变化趋势。

(4) 判据中的S的右半平面指的是开右半平面，不包括虚轴。

(5) 若Nyguist图正好通过(-1，j0)点，则闭环系统存在虚轴上的极点，计算N时不视为一次包围。如果求得Z=0，则闭环系统临界稳定。

(6) Nyquist图会同时存在既有逆时针包围又有顺时针包围(-1，j0)点的情况。N>0表示逆时针包围(-1，j0)点N圈，N