[科普中国]-基于改进稀疏表示法的谐波源定位

背景

谐波源的定位是解决谐波潮流计算、划分各谐波源谐波责任和采用经济手段惩罚谐波问题的基金项目：国家自然科学基金项目(50877068，51207130)；中央高校基本科研业务费专项资金项目(SWJTU11ZT07)。Project Supported by National Natural Science Foundation of China(50877068, 51207130); Project Supported by the Fundamental ResearchFunds for the Central Universities(SWJTU11ZT07).基础，具有重要意义。谐波源定位方法可归为2类 ：1

一类为基于等效电路模型的定位法，该类方法原理简单，但定位结果误差大；

另一类为基于谐波状态估计的定位法，该类方法量测数量少，定位结果精确，是当前的研究热点。谐波状态估计是谐波潮流计算的逆过程，其最终目的是要识别系统中谐波源的位置、类型以及大小。2

谐波源定位原理1、概述

在谐波状态估计中，一般选取节点的谐波电压作为量测量，节点的谐波注入电流作为估计量(状态变量)。则基于谐波状态估计的谐波源定位依据负荷向系统注入谐波电流的正负及数值大小来判断负荷是否为谐波源。

通过估计网络的谐波注入电流来确定谐波源的位置。网络节点的数量越多，所需的量测节点数越多。因此，在进行谐波源定位时，先初步判断存在谐波源的嫌疑区域。嫌疑区域的划分借鉴了配电网故障定位分区的思想 。以常开型联络开关为界将配电网络分成许多小区，根据各个联络开关谐波电流信息粗略判断出存在谐波电流的嫌疑区域，然后再进行定位。1

一些负荷虽存在谐波注入电流，但其数值微小，对电网的污染可忽略不计。因此，当负荷向全网注入的谐波电流为正且大于一恒定值时，该负荷为谐波源；否则，该负荷为非谐波源。

2、基于最小二乘法的谐波源定位原理在谐波状态估计算法中最有生命力的是最小二乘估计算法及其延伸算法。基于最小二乘法的谐波源定位是基于谐波潮流计算的逆过程。嫌疑区域中各节点谐波电压和谐波注入电流的关系为

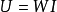
式中：

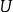——为嫌疑区域中各节点的谐波电压；

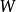——为线路阻抗组成的矩阵；

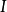——为嫌疑区域中各节点的谐波注入电流。

3、基于稀疏表示法的谐波源定位原理

在电力系统中，追求用最少的量测节点最准确地估计出各个节点的谐波注入电流，进而定位出谐波源。

量测点数 m 要多于同时出现谐波源的最大数量 s，即 m>s。由于电力系统谐波源分布存在空间稀疏特性，因此将信号处理的稀疏表示法应用到谐波源定位中。

基于稀疏表示法的谐波源定位可通过 m 个量测点对 p 个嫌疑节点的谐波注入电流进行估计。这使得在 p>>s 的工况下，可通过非常少的量测点完成谐波源的定位。

由于嫌疑节点谐波注入电流组成的列向量为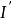 ，则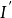与 s 的关系为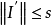： ，即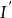的 0 范数在 s 以内。即可转化为非线性优化问题：

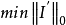
定义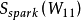 为矩阵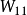 的最小线性相关列数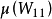， 为格莱姆矩阵 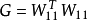中最大的非对角元素， 为估计精度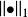， 为向量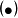 的1范数，若量测矩阵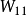满足唯一性和等价性的 2 个条件，谐波源的定位可转化为线性优化问题，即转化为

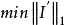
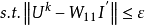可见，解的唯一性需满足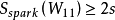，解的等价性需满足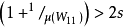。1

基于改进稀疏表示法的谐波源定位1、基于稀疏表示法的量测配置算法

量测矩阵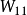的选择决定着稀疏表示法在谐波源定位中的有效性和准确性，因此量测节点的选择显得非常重要。

一般情况下，根据嫌疑区域电网的用电情况，可得到同时出现谐波源的数量s。基于稀疏表示法的量测配置算法，就是在确定嫌疑区域同时出现谐波源的数量 s 的情况下，寻找量测节点集合中满足条件

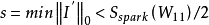尽可能小的子集，实现系统的完全可观测。

的边界条件可简化量测配置问题，即

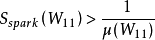
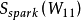配置过程中如能使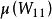的值尽可能小，的值就会尽可能大，进而极大限度地保证系统可观性。量测配置步骤如下：

1）确定同时出现谐波源的最大数量s和量测配置的数量M，形成各次谐波的导纳矩阵。

2）根据网络的拓扑结构和导纳矩阵，确定待选的量测矩阵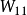。将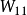中的各列向量归一化，并计算出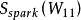和。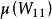

3）在待选的量测矩阵中，逐一去掉一个量测节点。如果某量测节点的删除使得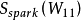的增幅最大且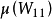的增幅最小，则将该节点排除在量测节点的范围外。

4）重复步骤 2）—3），直到量测配置减少到预先设置的数量。

5）对于所考虑的各次谐波，重复步骤 1）—4）。1

2、基于改进稀疏表示法的量测配置优化算法

在稀疏表示法中，不同量测节点的配置会影响定位结果的精确性。若单纯地根据网络的拓扑结构和导纳矩阵来选择量测节点，则忽视了嫌疑区域中其他非谐波源节点存在干扰噪声的实际情况。而干扰噪声的存在，极易导致系统不能完全可观，进而使得不能准确定位出谐波源。

基于改进稀疏表示法的谐波源定位，实质上是用2次稀疏表示法来对谐波源进行定位，其目的是排除非谐波源干扰电流的影响。通过初次的稀疏表示法得到谐波源电流估计结果，缩小谐波源的嫌疑区域；然后进行量测节点的相应调整，有针对性地进行二次稀疏表示，从而根据各个节点的谐波电流大小得出谐波源的位置。

因此，将量测节点配置进行以下优化：

根据网络的拓扑情况初步选择量测节点，来稀疏表示整个嫌疑区域节点的谐波注入电流；根据初次估计的电流结果，调整相应的量测节点，来排除干扰噪声的影响。量测节点的选择不仅要根据网络的拓扑结构来尽量满足稀疏表示的唯一性和等价性，而且要根据初次估计的电流结果来尽量使其安装在极有可能为谐波源的节点上。1

优点针对谐波源随机分布及非谐波源节点存在干扰电流的情况，使用基于改进稀疏表示法的谐波源定位。仿真结果表明，该方法的定位精度优于最小二乘法和稀疏表示法，适用于多谐波源的定位；具有良好的抗噪声干扰能力，可用于谐波源随机分布时的情况。1