[科普中国]-噪声载荷

相关背景

结构在随机振动载荷作用下会产生随机振动。宽带、中高频随机振动载荷可以激发起结构的多数模态参与振动，在某些频率上产生足够大的应力，从而导致结构的高周疲劳失效。这类问题最典型的代表是航空飞行器结构(飞机及发动机)中的声疲劳问题。声疲劳是结构在声载荷的激励下，因结构中快速交变应力作用，致使结构产生疲劳破坏的现象。这种快速交变应力是由噪声激励引起结构振动而产生的。噪声对结构的作用本质上是一种空间分布的，并且具有一定频率分布特性的动态随机压力载荷。这种载荷超过一定量值后，如声压级超过140dB，便可能对结构产生较大激励，特别是当噪声的频率分布特性和结构的动态特性相近时，结构就会产生显著的应力响应。在这种动态应力的长时间作用下，如同一般的振动疲劳问题一样，结构上应力集中和其他缺陷部位就会产生疲劳裂纹直至发展为疲劳破坏。这就是所谓的结构声疲劳问题。如果声压级超过180dB时，还可能产生足以导致结构迅速破坏的高强声载荷。航空发动机是一个非常强大且复杂的噪声源，处于这种宽频带高能级声激励环境中的构件极易发生高频疲劳。

声激励作用下的结构振动应力研究是声疲劳分析的基础，因此在航空发动机结构设计过程中进行引起声疲劳的随机振动应力估算是进行抗声疲劳设计的重要组成部分。因此开展声激励作用下薄壁壳体构件的应力响应估算具有重要意义。

噪声载荷研究现状飞行器在飞行过程中，声源在运动，飞行器的飞行速度，飞行姿态和发动机的功率状态都在变，因而，声源强度、飞机位置以及不同几何关系等所有的量都在随时间变化。

薄壁结构在噪声载荷下的动态响应分析，目前较为普遍采用的研究方法如下:

1)数值积分法

2)有限元素方法

3)模态叠加分析法

4)统计能量分析方法(SEA)

苏志敏等对噪声载荷作用下结构动力学响应有关的数值积分法、有限元素法、模态分析法及统计能量分析(SEA)法等研究方法进行了详细总结。目前对噪声载荷下薄壁结构的随机振动响应的研究工作主要分为两步:1)确定噪声的载荷;2)估算噪声激励作用下薄壁结构动态响应。

费志中、李辉荣、张冬梅等应用多种方法对复合材料层合板在噪声载荷作用下的力学响应进行了分析。A.G. Radu等提出一种降阶模型基于MSC.NASTRAN程序对热声祸合激励下的飞机面板组件进行疲劳寿命预测和动态响应分析。V. Crupi提出一种将不同的结构失效模型相统一的分析方法，并用该方法对结构的阻尼进行分析，建立了材料的内部阻尼与高周疲劳极限之间的联系。Robert W. Gordon和Joseph J. Hollkamp指出对结构进行声载荷响应预测时如果忽略结构与声介质之间的祸合作用会带来很大的误差，同时针对声响应预测提出一种改进方法，该方法利用结构/声系统祸合复模态将模型降至低阶，并且通过该方法预测了声/固祸合系统的非线性随机响应。Adam J. Culler开发了一种流热固祸合分析方法进行瞬态气动加热和波动压力(包括边界层湍流和发动机噪声共同激励产生的波动压力载荷)祸合载荷下的响应预测，通过该方法对C/C高超声速飞行器蒙皮壁板进行准静态和动态响应分析。R. Perez等论证了一种热弹性降阶模型(thermoelastic ROMs )，利用该模型对热载荷和声载荷下的各向同性面板和功能梯度材料面板进行几何非线性响应和温度响应分析，结果表明，该模型的分析结果与有限元法分析结果有很好的一致性。

对于功能材料，贺尔铭、胡亚琪等人利用ANSYS有限元方法对FGM进行了不同条件下的分析。杨智春、高扬等基于Marguerre曲板理论、von Karman大变形理论和气动力活塞理论建立超音速气流中三维复合材料曲臂板的有限元模型。分析了不同边界条件下复合材料曲臂板的曲率对颤振边界特性的影响规律。对于超音速飞行器的壁板颤振分析，Bein等人通过盖勒金方法和偏微分方程，得到了薄板颤振模态祸合的非线性方程，通过欧拉方程得到的结果与三阶活塞理论中得到的进行比较，符合结果很好。苏睿、吕高辉、朱红红等研究了含缺陷复合材料层合板的疲劳问题，并没有声载荷;于锋礼、沙云东、唐金等研究了噪声载荷下金属材料的疲劳。

噪声来源飞机在飞行过程中，噪声来源主要有以下几种:1.动力系统工作产生的噪声，如喷气噪声、涡轮风扇及压气机噪声、螺旋桨噪声等;2.飞行中空气动力产生的噪声，如附面层压力脉动、空腔噪声、分离流噪声、激波振荡噪声等;3。武器系统发射产生的噪声。

声疲劳问题噪声疲劳，也称声疲劳，是飞机结构在使用过程中经常遇到的一种疲劳损伤，是结构在声载荷的激励下，因结构中快速交变应力作用，导致结构产生疲劳破坏的现象。这种快速交变应力是由噪声激励引起结构振动而产生的。对由声激励载荷引起结构的振动发展而来的声疲劳技术和由结构振动辐射到周围介质的声能发展来的声辐射技术圈的研究，是现在航空航天领域研究的两大课题。从结构使用的可靠性角度出发，声疲劳问题更加突出。

作用在飞机薄壁结构上的噪声载荷在时间和空间上是随机分布的。当这种载荷的量值相对较小时，尚不会对结构产生影响;但随着声载荷量值的增大，结构上就会产生一定的分布应力响应:特别是当噪声的频率分布特性和结构的动态特性互相祸合时，结构就会发生显著的应力响应。在这种动态应力的长时间作用下，就如同一般的振动疲劳问题一样，在结构上应力集中或其它缺陷部位处会产生疲劳裂纹直至发展为疲劳破坏。这就是所谓的结构疲劳问题。

实践表明，不论是军用还是民用飞机，在使用中都会常常出现各种类型的声疲劳破坏现象。其中大多数表现为:各种翼面蒙皮及机身侧壁蒙皮裂纹、掉铆钉，甚至发展到相应的翼肋和机身环框裂纹;进气道内蒙皮裂纹、掉铆钉和相关结构损坏;燃烧室及机尾结构在喷流热噪声联合作用下产生的各种破坏现象等。尽管一般认为，这类问题可以被早期发现、修理，不可能导致重大的飞行事故。但如果不在设计、研制中较好的解决这一问题，仍将会给飞机使用带来极大的不方便并将付出可观的维修费用。此外，产生结构疲劳的部位，由于存在强烈的噪声和振动，往往会引起邻近安装的机载设备系统的失灵及其它破坏现象，影响到机载设备的可靠性和飞行安全。

噪声载荷下结构的疲劳寿命分析方法飞行器结构噪声的疲劳研究涉及到声学工程、材料特性、机械振动、生产工艺、疲劳等相关学科领域，其研究的范围主要包括噪声特性分析、噪声源、结构的声疲劳特性分析、结构声疲劳试验技术研究、结构动力学特性分析及其优化设计等。

目前，国内外对飞机薄壁结构的声疲劳问题做了一些研究，主要有两个己知的声疲劳寿命评估算法。第一个是时域分析，利用周期计数的数值方法，即雨流循环计数方法，涉及较长的应力时间历程，统计需考虑应力的峰值或谷值，计算疲劳损伤和结构的使用寿命，但该方法非常耗时费力。另一个是基于所谓光谱的频域分析方法，其中不规则的应力响应建模为一个随机过程。基于光谱的方法利用解析公式关联的雨流循环分布，疲劳损伤与疲劳寿命的功率谱密度的过程。相比于疲劳寿命评估时间域的方法，尤其是在结构设计阶段更容易且更快。另外，频率域声疲劳计算可以用功率功率谱密度(PSD)在随机载荷与响应之间建立一个线性传递函数。除理论方法外，大量的实验归纳总结出多种算法并应用到工程实际中。

对于飞行器结构进行声疲劳分析，一般程序如图所示。1

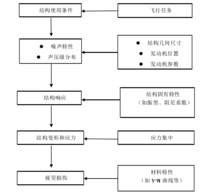
薄壁结构在声载荷下动态响应的研究方法确定噪声载荷的方法噪声载荷的确定是研究声激励下薄壁结构动态响应的前提。然而，实际过程中的噪声是随空间和时间随机变化的，因此实验测量成为确定噪声的主要方法。关于噪声载荷的研究，北京航空航天大学的周盛教授、孙晓峰教授、王同庆教授等对此都作了大量的工作，同时也取得了很大的成绩。沈阳航空工业学院的盛元生教授和沈阳航空发动机设计研究所的有关专家对发动机燃烧室的噪声进行了多次测量，奠定了认识燃烧室噪声场的基础。

实际过程中由于某些结构的复杂性和工作环境的特殊性，仅仅通过实验测量的数据不足以代表结构件本身的噪声载荷。因此必须与理论分析相结合，通过必要的假设模拟出整个结构的噪声载荷情况，即建立符合实际的噪声载荷模型。

动态响应由于薄壁结构受到的声载荷是一个随机载荷，加上其内部不但有平面声波而且还有高阶声模态，这就使得求解随机载荷对薄壁结构响应问题变得非常复杂。国内外许多学者在这方面作了大量的理论与实践研究。目前较为普遍采用的主要研究方法如下：

(1)模态叠加分析法

模态叠加分析法是研究时不变线性系统随机振动响应的有效方法，它是将系统的响应表示成各模态响应的加权和，也就是各模态对于系统响应的贡献量的叠加。Miles是最早应用模态叠加分析方法做此项研究的学者之一。随后Powellclarkson，也都提出了自己在这方面的研究观点。

(2)数值积分法

应用数值积分法研究随机振动的动态响应也很受人们的关注，它主要是通过一些数学方法对响应进行时域或频域上积分而获得最后的结果。其中Monte Carl。法是时域积分法中经常使用的一种方法。时域Monte Carl。法，可以用来解决非线性系统随机激励响应。它可以用于解很多具有概率性质的问题，广泛应用于解非线性、非匀质和时变材料特性、非平稳、非均匀输入等问题。

(3)统计能量分析方法(SEA)

统计能量分析(SEA)方法是运用能量流关系式对复合的、谐振的组装结构进行动力特性、振动响应级及声辐射的理论评估。主要是应用此方法估算高频区域的声激励响应。陕西机械学院的马建敏等人用统计能量分析(SEA)法研究了在高频宽带随机噪声场中板及加筋板(航空航天用蒙皮)的加速度响应。

(4)有限元素方法

现今越来越多的人利用有限元素法来解决工程中的许多问题，这也包括了薄壁结构在噪声载荷下的振动响应问题。有限元素法是根据变分原理求解数学物理问题的一种数值方法。其力学基础是弹性力学，而方程求解的原理是采用加权残值法或泛函极值原理，实现的方法是数值离散技术，最后的技术载体是有限元分析软件。一般而言，其基本思想为:结构离散、单元分析、总刚集成、载荷移植、约束处理及求解方程组。尽管利用有限元素法来分析问题存在以下不足:一是实际结构的简化模型及其边界条件的模拟不能做到完全反映实际情况;二是其对计算机硬件和有限元分析软件依赖过大。但是由于其理论和分析软件随着计算机发展的巨大进步，人们对其的偏爱也愈发明显了。由此可以肯定有限元素法将会成为今后解决有关薄壁结构振动响应的主流方法。2